くわっど は ぜんご じょうげ さゆう の えりあ \(^▽^)/
この ページ は 現在 32% クオリティyone12053.zouri.ne.jp
〒1v3-0vv0 東v都○○区○○○1-v-3
8くわっど に ついて ..
4くわっど へんしゅうちゅう ( 前 後 左 右 上 下 )
| 【 前・後・上・下・左・右 】 りろんじょう の すうち や データ ではなく、はこ や たてもの のように じっさい の かたち に さいげん しながら かくにん できる のが この【 前・後・上・下・左・右 】の コーナー になります。ぶんみゃく によっては 「 たて よこ おく 」 などと かかれる ことが ありますが、きほんてき に おなじこと になります。ほとんど の ないよう は 、はこ の カド が スタート ちてんに なり、そこから その「 つい になる カド 」 まで ついて かんがえます。つまり はこ の「 カド から カド までの はなし 」といえます。 この ページ は あお いろ なので、おもに、シミュレーション に よる ぐたいてきな データ ( さんこうけっか・サンプル ) を あつめます。そこから みえてくる ケツロン ( きょうつうてん ) を さがしていきます。 |
  |
ページ ないに げんざい ある こうもく (要編集 要移動 要修正)
■ ぎゃくほうこう ■ もとにもどる ■ マイナス ほうこうへんかん
■ まえ0cm…90ど ■ ほぼ 90ど ひらく ■ 90ど よりもひらくエリア
■ かくだい・たんい ■ 4つ の ミラー∠ みひらき ■ 14/17 こうもく マイナス OK
■ 3 こうもく マイナス せなかあわせ ■ まえ4クワッド ■ うしろ4クワッド
■ きょくたんにおおきいあたいがあるときの みひらき
■ たかさがきょくたんにひくいときの みひらき → ほぼ2Dとおなじ
■ たかさが0だと → へいめん ■ ぜんごで みてみる コサイン
■ 90ど ちかく ∠それていても すすむのか?
■ 未 ■ 未 ■ 未 ■ 未
ナビゲーション
. |
『 quad 』 の かんれん わーど |
◆ 「 マイナス 」 なら 「 ∠ 180 ど 」 それた ほうこう
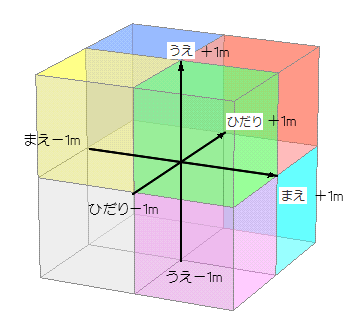 |
ぎゃく ほうこう は 「 180 ど 」 こちら ( → 信 ) の ていぎ により つぎ の こと が いえます。
に なります そのほか の いいまわし ( → 知 ) |
||||
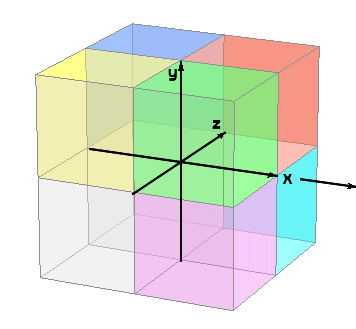 |
もとに もどる こちら ( → 信 ) の ていぎ により つぎ の こと が いえます。 ま え に 6cm すすんだ あと ⇔ うしろ に 6cm すすむ う え に 2 m すすんだ あと ⇔ し た に 2 m すすむ ひだり に 3km すすんだ あと ⇔ み ぎ に 3km すすむ これら は もとの ばしょ ( げんてん ) に ぴったり もどります。 これら を 100 回 くりかえしても 1mm の ブレ なく もとに もどります。 ( ユークリッド ) |
||||
 |
「 マイナス ほうこう 」 は 「 ぎゃく ほうこう 」 ◆ う え に マイナス 1 センチ = し た に 1 センチ ◇ し た に マイナス 2 センチ = う え に 2 センチ ◆ み ぎ に マイナス 3 センチ = ひだり に 3 センチ ◇ ひだり に マイナス 4 センチ = み ぎ に 4 センチ ◆ ま え に マイナス 5 センチ = うしろ に 5 センチ ◇ うしろ に マイナス 6 センチ = ま え に 6 センチ さへん と うへん は おなじ いみ に なります |
||||
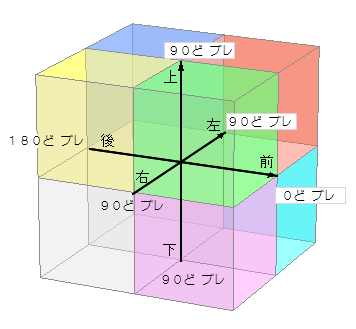  |
ぜんご の うごき が ぜろ cm なら ⊥ 90 ど こちら の ていぎ に より ( → 信 ) ぜんご いどう が まったくなく、 ぜろ cm、 ( で じょうげ さゆう に わずか でも いどう していれば ) くうかん かくど は 「 ⊥ 90 ど 」 の ひらき になります。 れい 前後 上下 左右 ( ぜろ cm , -2 cm , -1 cm ) 前後 上下 左右 ( ぜろ cm , 4 cm , -777 cm ) 前後 上下 左右 ( ぜろ cm , 500 cm , 0 cm ) これら ↑ は まよこ へいめんじょう の いち なので、いずれも 「 ⊥ 90 ど 」 の ひらき になります。 |
||||
 |
ぜんご の うごき が ぴったり ぜろ cm では ないにしても … 「 ほぼ ぜろ cm 」 なら ほぼ ⊥ 90 ど ぜんご の いどう が ぴったり ぜろ では ないにしても … 0.0001 や 0.00002 cm など の ように、 たて や よこ とくらべて 2 ケタ くらい ちがうような .. あっとうてき に ちいさいとき は けっかてき に くうかん かくど は 「 ほぼ ⊥ 90 ど 」 の ひらき になります。 れい 前後 上下 左右( -0.01 cm , -2 cm , -1 cm ) ∠ 90.3 ど 前後 上下 左右( 0.002 cm , 4 cm , -777 cm ) ∠ 89.9 ど 前後 上下 左右( -0.0003 cm , 500 cm , 0 cm ) ∠ 90.00003 ど 前後 上下 左右( 0.00004 cm , 500 cm , -777 cm ) ∠ 89.99999 ど |
||||
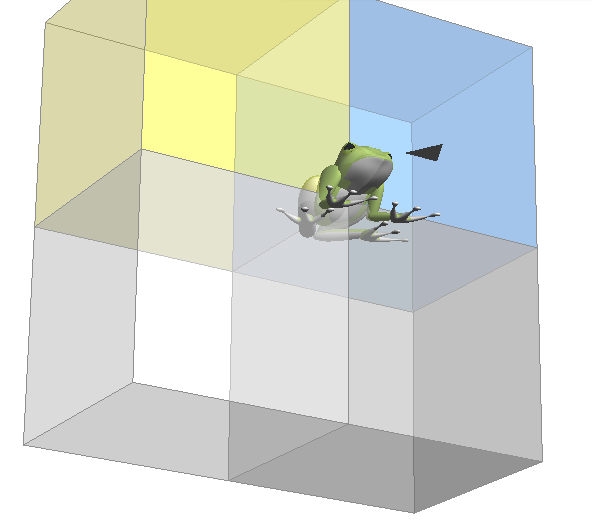  |
わずかでも 「 うしろ 」 なら かならず 90 ど いじょう わずかでも うしろがわ に ふりむいている なら その ∠ みひらき は かならず 90 ど ( すいちょく ) よりも おおきく ひらきます。 れい
「 うしろ 」 エリア なら かならず 90 ど いじょう に なります。 まよこ ( や まうえ ) が 90ど に なり それよりも うしろ の 4 ブロック の エリア なら それる カクド が 90ど よりも おおきく なります。 カクド 値 は おおよそ に なります。 ( ぴったりでは ありません ) |
||||
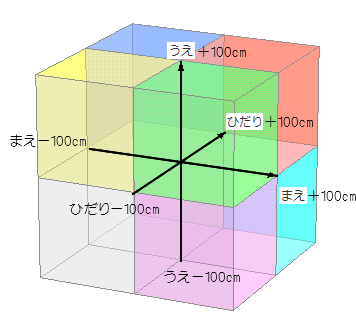 |
( ながさ の ) 単 位 が かわっても カクド は かわりません 1m が 100 cm の きざみに なっても ひりつ が おなじ なので ∠カクド は かわりません。 ( まえ 2 m , ひだり 2 m ) の かくど は ∠ 45 ど ( まえ 2 cm , ひだり 2 cm ) の かくど も ∠ 45 ど ( まえ 2 km , ひだり 2 km ) の かくど も ∠ 45 ど ( まえ 2 インチ , ひだり 2 インチ ) の かくど も ∠ 45 ど ( まえ 2 ヤード , ひだり 2 ヤード ) の かくど も ∠ 45 ど ( まえ 2 マイル , ひだり 2 マイル ) の かくど も ∠ 45 ど かくだいコピー しゅくしょうコピー の ような かんじに なります ( そうじ ずけい ) 3じげん ( はこがた ) でも これは かわりません。 要実例 追加 へんかんりつ → 知 |
||||
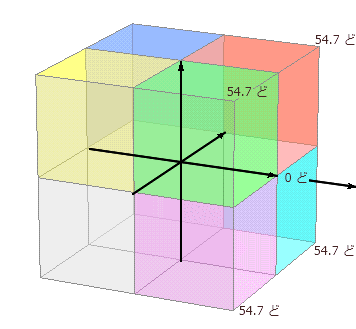 → 54.735 ° |
ミラー・さかさ は ∠ おなじ 「 まえ 」 を 0 ど ( もくひょう ) に するなら、 じょうげ と さゆう は プラスマイナス ぎゃく でも それる かくど は おなじ に なります xyz( 100, 100, 100 ) ∠ 54.7 ど xyz( 100, ー100, 100 ) ∠ 54.7 ど xyz( 100, 100, −100 ) ∠ 54.7 ど xyz( 100, ー100, −100 ) ∠ 54.7 ど じょうげ さゆう ミラー の ∠ ほうこう に なります はこ の かど である ひつよう は ありません。 ∠0 ど ほうこう ( まえ ) を ちゅうしん に みぎ と ひだり の はば cm が うえ と した の はば cm が おなじなら ∠ おなじ に なります。 |
||||
| 【 重 要 】 こちら 考: 8カンスウ ( 17 こうもく ) の うち θ j xij θ Ψ θ 山 θ Φ θ 巾 θ R 山 巾  マイナス 値 が ∠ みひらき カクド に えいきょう を あたえる のは ..  この 3 こうもく だけ に なります。 いいかえると、 17 こうもく 中 14 こうもく は プラス と マイナス は ( ミラー の ∠ みひらき で ) おなじ カクド ( けっか ) を だします。  ( クリック ) この 14 こうもく は ∠ ± ミラー たいおう OK ↓ 3 こうもく に ついて .. |
|||||
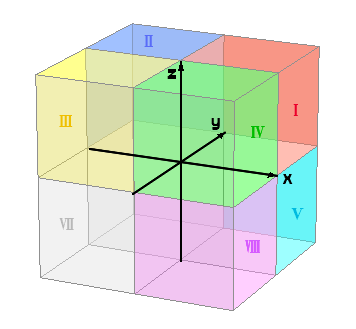 |
この 3 こうもく だけは  えっくす ふぁい あーる マイナス の とき ∠ せなか あわせ で でてきます。 
で でてきます。 ぜんご たいしょう ( まえうしろ ミラー ) な ことが わかります。 → 知: ほかく → 思: マイナス おそるることなかれ |
||||
 |
こちら 、おおきくとも … ∠ みひらき が 90ど いない に なります。 ■■■■ すくなくとも まえ に すすんで いる ことに なります おおきくとも ∠ みひらき が 90ど いない に かならず なります |
||||
 |
こちら 、すくなくとも … ∠ みひらき が 90ど いじょう に なります ■■■■ すくなくとも うしろ に すすんで いる ことに なります すくなくとも ∠ みひらき が 90ど いじょう に かならず なります |
||||
 |
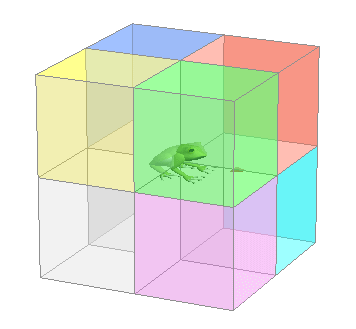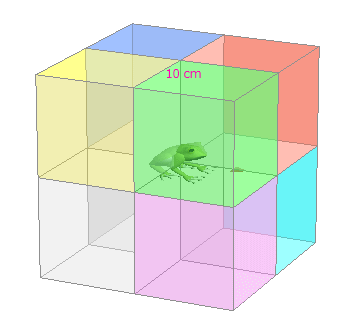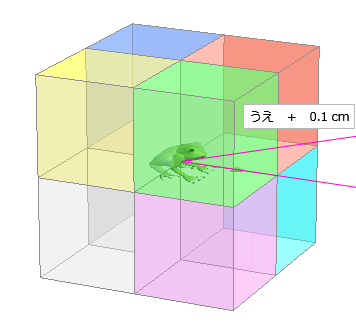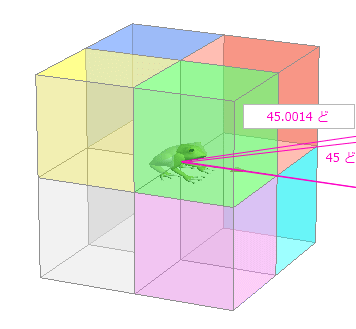
x y z の どれか ひとつ の じく の あたい が ほか の ふたつの じく の あたい とくらべて きょくたん に おおきい と そっち の じく に ひっぱる ちから が ケタ はずれ に つよい ので ( およそ ) 90ど の ばいすう に なります xyz(−2, 777, 3 ) ∠ 90.15 ど xyz(−1, 2, 888 ) ∠ 90.06 ど xyz(−9999, 1, 1 ) ∠ 179.99 ど ( ほぼ 180ど ) xyz( 10 億 , ー100, −100 ) ∠ 00.00001 ど ( ほぼ 0ど ) じく ライン の ふきん に ある ことが わかります |
||||
 |
2じげん と 3じげん で ほとんど ∠ カクド が かわらない のは どういうとき ? まえ に 10 センチ 、 よこ に 10 センチ は へいめん の 2 じげん で ∠ 45 ど に なります。 が、 ここに たかさ が わずか に 0.1 センチ くわわり 3じげん に なると ∠ カクド は どうなるか みてみました。 2じげん ( へいめん ) と かなり ちかい カクド に なります。 |
||||
| ななめ 5 cm 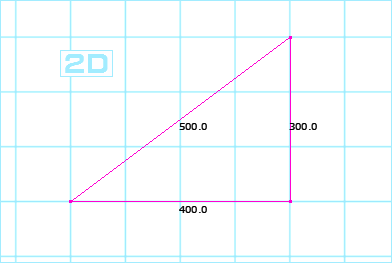 かくだい ななめ 5.03 cm 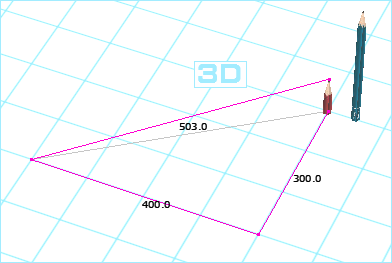 えんぴつ 5.4 mm |
3じげん の ななめ の ながさ に ついて ( 3 じげん め ) たかさ が ゼロ に ちかい なら 2じげん の ななめ の ながさ と かなり ちかく なります ひだり の ず は うえが 2D したが 3D になります。 したの ず に ある ちびった えんぴつ の たかさ を もとめてみます 3 cm × 3 cm + 4 cm × 4 cm + え cm × え cm = 5.03 cm × 5.03 cm 9 cm2 + 16 cm2 + ( え cm )2 = 25.3009 cm2 25 cm2 + ( え cm )2 = 25.3009 cm2 ( え cm )2 = 0.3009 cm2 え cm = 0.3009 cm2 の るーと え cm = 0.548.. cm 3じげんめ の たかさ ( あたい ) が ちいさい なら その くうかん きょり は わりと ちかくなる ことが わかります。 ←↑ この ず の ひりつ の ばあい 3じげんめ を こうりょ した ばあい と しなかった ばあい は 5 : 5.03 = およそ 99.4 % となります。 |
||||
 |
まえ を 0ど と したとき の エリア べつ こさいん 値 いわゆる ぜんぽう の 4 エリア の ■■■■ の いずれか の かくど で こさいん を すると すくなくとも プラス 値 に なります ( ※ 90じく の しゅんかん は プラスマイナス ゼロ ) ぎゃくに いわゆる こうほう の 4 エリア の ■■■■ の いずれか の かくど で こさいん を すると おおきくとも マイナス に なります ( ※ 90じく の しゅんかん は プラスマイナス ゼロ ) |
||||
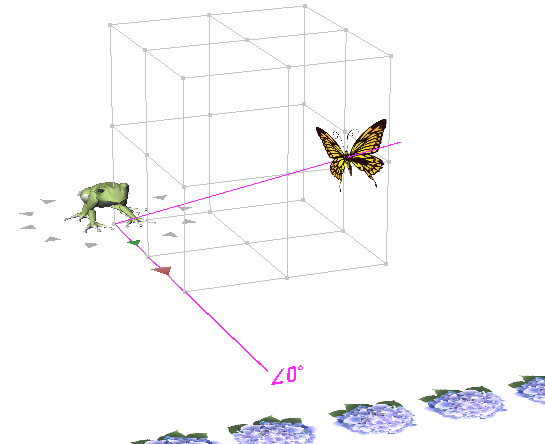 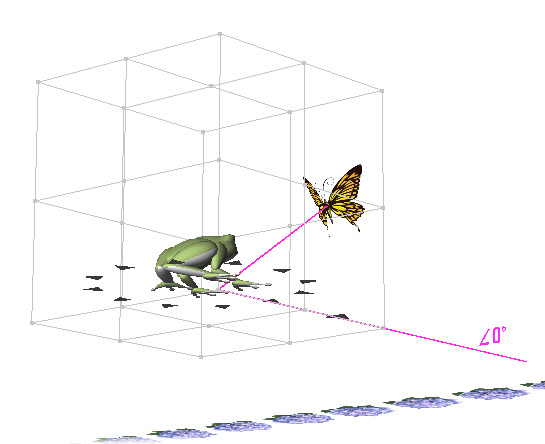 |
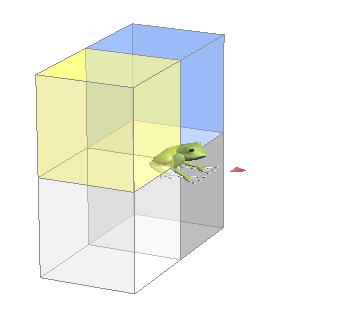
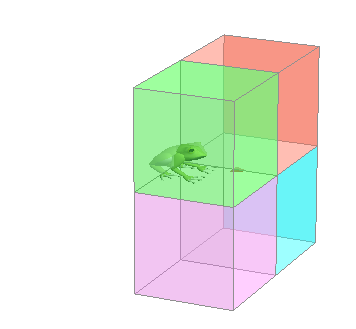
( こちらの 「 やくそく 」 を 信 じる : として .. ) ほぼ へいこう の ∠89 ど ズレ 、 いつ .. ?、たどりつくの ?.. か .. ( → 思 : ムダ に かんじられる とりとめのない どりょく ) はたして、むくわれる のだろうか .. 1 ÷ こさいん ( ∠カクド ) = なんばい にて、けいさん してみます ..。 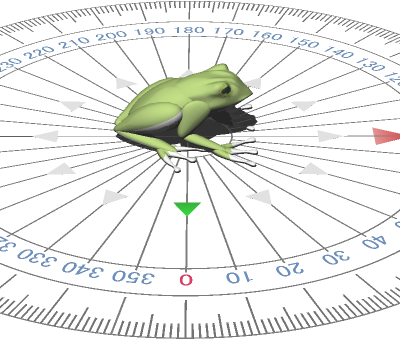 → → → … ・・ → → → … ・・カエル が もくてき ( アジサイ ) に たいして ほぼ へいこう の かくど
これだけ ∠ ブレ てても、 けいさんじょう は たどりつく ことが わかります。 1 ÷ こさいん ( ∠カクド ) = なんばい 考 : 1m さき の アジサイ 信 : かだん に おわり は ない 思 : むりっぽく ない ? |
||||
| |
|||||
もどる
( 知 思 分 信 考 )
copyright©2022 Render view all rights reserved.