�₵��@�Ɓ@�邢�@�@�́@�@���������@�b�@!!�@�@�@�@�_(^��^)�^
���� �y�[�W �� ���� �Q�� �N�I���e�Byone12053.zouri.ne.jp
��1v3-0vv0 ��v�s�����恛����1-v-3
�[ �₫�イ �S �[�@�@�@�����イ ������

�y�[�W�@�P�@�Q�@�R�@�S
�₫�イ �ɂ�����@�����イ �� �J�N�h�@�� �� �� �J�N�h �P �� �F�@�`�����O���[�h �i cho�� �j �ɂā@�ǂ��� �Ɂ@������@���Ă݂܂��B �@���@�Ɓ@ ���@�Ɂ@���� �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�@�@�@�y�[�W�@�Ȃ��@�́@��������
�@�@�@�@�邢�@�@�₵���@�@���ǂ�
�@�@�@�@(�@�ׂ@�́@�y�[�W�@���������@( �t���C�E�S�� ))
�x�[�X�@�Ȃǁ@�@�@�@�@�@�@�@�@�@�@�@�@�@ �� ���傤�����@�@�� ���ǂ�
�~�[�g�|�C���g�@�́@�������@�́@����Ɂ@72.5 cm�@�Ɂ@���Ă��܂��B�@m(_ _)m�t�@�[�X�g�x�[�X�@�@22.550610134864�@cho���@(��)
�Z�J���h�x�[�X�@�@ �@ 5.005090907090�@ cho��
�T�[�h�x�[�X�@�@�@�@27.540319164167�@cho���@(��)
�z�[���x�[�X�@�@�@�@55.000000000000�@cho��
�Ƃ������@�@�@ �@ 5.008020703070�@cho���@(��)
�@�t�@�[�X�g�x�[�X�@�@�@�@22.550610134864�@cho�� �@ �@�@���C�g����@�Ȃ̂Ł@�ӂ�ނ��@ �́@ �� �| 45�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �|1.54�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|1.5374793333844532911078686584341�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos - 45���@�~�@cos - 1.54�� ) �@�@�@�@�@�@�@�@���@acos ( 0.707..�@�@�~�@0.999.. ) �@�@�@�@�@�@�@�@���@acos ( 0.706.. ) �@�@�@�� cho �R�@���@45.02�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign ( - �� )�@ �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@tan - 1.54���@���@|�@sin - 45��| ) �~ sign (-(-45)) �{�@( 180�� �{180���~ sign (- 45��)) ���@acot (�@- 0.026..�@�@���@| - 0.707..�@|) �~ sign ( 45�� )�@�{�@( 180�� �{�@180���@�~ ( �|�P )) ���@acot (�@- 0.026..�@�@���@�@0.707..�@�@) �~ (�@�@1�@�@)�@�{�@( 180�� �|�@180���@�@�@�@ �@ ) ���@acot (�@�@�@�@�@�@- 0.037..�@�@�@�@�@ ) �~ (�@�@1�@�@)�@�{�@( �@�@�@�@�@0���@�@�@�@�@�@ ) ���@acot (�@- 0.037..�@)�@�{�@�@0�� ���@(�@�@- 92.17��..�@�@)�@�{�@�@0�� �@�� cho ���@���@92.17�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� ( 45.02���@���@18 ) ���Y �@���@�ځ@2.501145..�@���Y�@ �@�@�� cho ���@���@�� ( 92.17���@���@36 ) ��turn ���@�ځ@2.560383..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@2_.5_0_1_1_4_5.. �@�@�@�@ �� cho ���@�@2._5_6_0_3_8_3.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@ 22.550610134853..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�ځ@ 22.550610134864..�@cho�� �@ |
�@�Z�J���h�x�[�X�@�@�@�@5.005090907090�@cho�� �@ �@�@���傤�߂�@�Ȃ̂Ł@�ӂ�ނ��@ �́@ �Ɓ@�@0�@�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �|1.08�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|1.0796320253805541528037955407546�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 0���@ �~�@cos - 1.08�� ) �@�@�@�@�@�@�@�@���@acos (�@�@1�@�@�~�@0.999.. ) �@�@�@�@�@�@�@�@���@acos ( 0.999.. ) �@�@�@�� cho �R�@���@1.08�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign ( - �Ɓ@)�@�{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@tan - 1.08���@���@|�@sin�@0�� | ) �~ sign ( -(0��))�@�{�@( 180�� �{180���~ sign (�@0 �� )) ���@acot (�@- 0.018..�@�@���@|�@�@0�@�@ | ) �~ sign (�@0�� )�@ �{�@( 180�� �{�@180���@�~ (�@ 0�@)) ���@acot (�@- 0.018..�@�@���@�@�@0�@�@�@ ) �~ (�@�@0�@�@)�@ �{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@acot (�@�[���W���U�� �̂��� �ւ� ) �~ (�@�@0�@�@)�@ �{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@0�@�@�@�� �@ - 0.018..�@ ) �~ (�@�@0�@�@)�@ �{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@�@�@�@�@0�@�@�@�@�@�@�@ ) �~ (�@�@0�@�@)�@ �{�@( �@�@�@�@180���@�@�@�@�@) ���@(�@0���@)�@�{�@�@180�� �@�� cho ���@���@180�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� ( 1.08���@���@18 ) ���Y �@���@�ځ@0.059979..�@���Y�@ �@�@�� cho ���@���@�� ( 180���@ ���@36 ) ��turn ���@�ځ@5.000000..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@0_.0_5_9_9_7_9.. �@�@�@�@ �� cho ���@�@5._0_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@ 5.005090907090..�@cho�� ( ���肠�� �Ȃ� ) �@�@�@�@�@�@�@�@�ځ@ 5.005090907090..�@cho�� �@ |
�@�T�[�h�@�x�[�X�@�@�@�@27.540319164167�@cho�� �@�@���C�g����@�Ȃ̂Ł@�ӂ�ނ��@ �́@ �� �{ 45�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �|1.54�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|1.5374793333844532911078686584341�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 45���@�~�@cos - 1.54�� ) �@�@�@�@�@�@�@�@���@acos ( 0.707..�@ �~�@0.999.. ) �@�@�@�@�@�@�@�@���@acos ( 0.706.. ) �@�@�@�� cho �R�@���@45.02�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� ) �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@tan - 1.54���@���@|�@sin 45�� | ) �~ sign (-(45��)) �{�@( 180�� �{180���~ sign ( 45��) ) ���@acot (�@- 0.026..�@�@���@|�@0.707 .. | ) �~ (�@ �| �P �@) �{�@( 180�� �{�@180�� �~ (�@�P�@)) ���@acot (�@- 0.026..�@�@���@�@0.707..�@�@) �~ (�@ �| �P �@) �{�@( 180�� �{�@180���@�@�@�@ �@ ) ���@acot (�@�@�@�@�@- 0.037..�@�@�@�@�@�@) �~ (�@ �| �P �@) �{�@( �@�@�@�@�@360���@�@�@�@�@) ���@(�@�@�@�@�@�@�@92.17��..�@�@�@�@�@�@�@) �~ (�@ �| �P �@) �{�@�@360�� ���@( - 92.17��.. )�@�{�@360�� ���@�@ 360���@�@�@ �|�@92.17�� �@�� cho ���@���@267.82..�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� ( 45.02�� �@ ���@18 ) ���Y �@���@�ځ@2.501145..�@���Y�@ �@�@�� cho ���@���@�� ( 267.82���@���@36 ) ��turn ���@�ځ@7.439616..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@2_.5_0_1_1_4_5.. �@�@�@�@ �� cho ���@�@7._4_3_9_6_1_6.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@ 27.540319164156 ..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�ځ@ 27.540319164167..�@cho�� �@ |
�@�z�[���x�[�X�@�@�@�@55.000000000000�@cho�� �@ �@�@�܂����@�Ȃ̂Ł@�ӂ�ނ��@ �́@ �Ɓ@�@0�@�@�� �@�@�S���@�́@���� ���@�J�N�h�@�� �@ �� �|90�@�ǁ@�Ɂ@�Ȃ�܂��B �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 0���@ �~�@cos - 90�� ) �@�@�@�@�@�@�@�@���@acos (�@�@1�@�@�~�@�@0�@�@�@) �@�@�@�@�@�@�@�@���@acos (�@�@ 0�@�@ ) �@�@�@�� cho �R�@���@90�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� )�@�{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@ tan - 90�� �@ ���@|�@sin�@0�� | ) �~ sign ( -(0��))�@�{�@( 180�� �{180���~ sign (�@0 �� )) ���@acot (�@- 100000�@�@���@|�@�@0�@�@ | ) �~ sign (�@0�� )�@�{�@( 180�� �{�@180���@�~ (�@ 0�@)) ���@acot (�@- 100000�@�@���@�@�@0�@�@�@) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@acot (�@�[���W���U�� �̂��� �ւ� ) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@0�@�@�@�� �@ - 100000�@ ) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@�@�@�@�@-0�@�@�@�@�@�@�@) �~ (�@�@ 0�@�@)�@�{�@( �@�@�@�@180���@�@�@�@�@) ���@(�@0���@)�@�{�@�@180�� �@�� cho ���@���@180�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (�@90���@ ���@18 ) ���Y �@���@�ځ@5.000000..�@���Y�@ �@�@�� cho ���@���@�� ( 180���@ ���@36 ) ��turn ���@�ځ@5.000000..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@5_.0_0_0_0_0_0.. �@�@�@�@ �� cho ���@�@5._0_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@ 55.000000000000..�@cho�� ( ���肠�� �Ȃ� ) �@�@�@�@�@�@�@�@�ځ@ 55.000000000000..�@cho�� �@ |
�Ƃ������
�@�Ƃ������@�@�@�@5.008020703070�@cho�� �@ �@�@���傤�߂�@�Ȃ̂Ł@�ӂ�ނ��@ �́@ �Ɓ@�@0�@�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �|1.49�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|1.4892712890691328703734537726342�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 0���@ �~�@cos -1.49�� ) �@�@�@�@�@�@�@�@���@acos (�@�@1�@�@�~�@�@0.999..�@) �@�@�@�@�@�@�@�@���@acos (�@�@ 0.999..�@�@ ) �@�@�@�� cho �R�@���@1.49�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� )�@�{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@ tan-1.49�� �@���@|�@sin�@0�� | ) �~ sign ( -(0��))�@�{�@( 180�� �{180���~ sign (�@0 �� )) ���@acot (�@- 0.025..�@�@���@|�@�@0�@�@ | ) �~ sign (�@0�� )�@�{�@( 180�� �{�@180���@�~ (�@ 0�@)) ���@acot (�@- 0.025..�@�@���@�@�@0�@�@�@) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@acot (�@�[���W���U�� �̂��� �ւ� ) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@0�@�@�@�� �@ - 0.025..�@ ) �~ (�@�@ 0�@�@)�@�{�@( 180�� �{�@�@�@0���@�@ �@ ) ���@atan (�@�@�@�@�@�@�@-0�@�@�@�@�@�@�@) �~ (�@�@ 0�@�@)�@�{�@( �@�@�@�@180���@�@�@�@�@) ���@(�@0���@)�@�{�@�@180�� �@�� cho ���@���@180�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (1.49���@ ���@18 ) ���Y �@���@�ځ@0.082737..�@���Y�@ �@�@�� cho ���@���@�� ( 180���@ ���@36 ) ��turn ���@�ځ@5.000000..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@0_.0_8_2_7_3_7.. �@�@�@�@ �� cho ���@�@5._0_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�� �@ 5.008020703070..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�� �@ 5.008020703080..�@cho�� �@ |
�@�@�l�N�X�g�o�b�^�[�Y�@�T�[�N��
�@�@�P �邢����@�@62.165032917794 cho���@ cho���@(��)
�@�@�R �邢����@�@67.135937987295 cho���@ cho���@(��)
�@�P�@�邢�@����@�T�[�N���@�@�@62.165032917794�@cho�� �@�@�݂��ā@�ɂȂ�̂Ł@�ӂ�ނ��@ �́@ �� �|110.8�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �| 3.44�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|110.81083967238951683377838850656�� ) �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|3.4389148181361540220417809400913�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos - 110.8�@ �~�@cos - 3.44�� ) �@�@�@�@�@�@�@�@���@acos (�@- 0.355..�@�@�~�@0.998.. ) �@�@�@�@�@�@�@�@���@acos (�@- 0.354..�@) �@�@�@�� cho �R�@���@110.77..�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�@�� �@| ) �~ sign (�@- �Ɓ@)�{ ( 180�� �{180���~ sign (�@�Ɓ@ )) ���@acot (�@tan - 3.44���@���@|�@sin-110.8�� | )�~sign(-(-110.8��))�{(180���{180���~ sign (-110.8�� )) ���@acot (�@- 0.060..�@�@���@|�@- 0.934.. |�@ ) �~ sign( 110.8��) �{ ( 180�� �{�@180�� �~ (�@�|�P�@)) ���@acot (�@- 0.060..�@�@���@�@�@0.934..�@ �@) �~ (�@�@ �P�@�@) �{ ( 180�� �|�@180���@ ) ���@acot (�@�@�@�@�@- 0.064..�@�@�@�@�@�@ �@) �~ (�@�@ �P�@�@) �{ ( �@�@�@0�� �@�@ �@ ) ���@(�@�@�@�@�@�@�@93.67..���@�@�@�@�@�@�@�@) �~ (�@�@ �P�@�@) �{�@0�� �@�� cho ���@���@93.67�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� ( 110.77���@���@18 ) ���Y �@���@�ځ@6.153979..�@���Y�@ �@�@�� cho ���@���@�� ( 93.67�� �@ ���@36 ) ��turn ���@�ځ@2.602174..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@6_.1_5_3_9_7_9.. �@�@�@�@ �� cho ���@�@2._6_0_2_1_7_4.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@62.165032917794..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�ځ@62.165032918705..�@cho�� �@ |
�@�R�@�邢�@����@�T�[�N���@�@�@67.135937987295�@cho�� �@�@�Ђ���@�ɂȂ�̂Ł@�ӂ�ނ��@ �́@ �� �{110.8�@�� �@�@�S���@�́@���� ���@�J�N�h�@�́@ �� �| 3.44�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �{110.81083967238951683377838850656�� ) �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@( �� �|3.4389148181361540220417809400913�� ) �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos �@110.8�@ �~�@cos - 3.44�� ) �@�@�@�@�@�@�@�@���@acos (�@- 0.355..�@�@�~�@0.998.. ) �@�@�@�@�@�@�@�@���@acos (�@- 0.354..�@) �@�@�@�� cho �R�@���@110.77..�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�@�� �@| ) �~ sign (�@- �Ɓ@)�{ ( 180�� �{180���~ sign (�@ �� �@ )) ���@acot (�@tan - 3.44���@���@|�@sin 110.8�� | ) �~ sign(-110.8��)�{ ( 180�� �{180���~ sign ( 110.8��)) ���@acot (�@- 0.060..�@�@���@| �@ 0.934.. |�@ ) �~ ( �@ �| �P�@ ) �{ ( 180�� �{�@180���@�~ (�@�P�@�@)) ���@acot (�@- 0.060..�@�@���@�@�@0.934..�@ �@) �~ ( �@ �| �P�@ ) �{ ( 180�� �{�@180���@ ) ���@acot (�@�@�@�@�@- 0.064..�@�@�@�@�@�@ �@) �~ ( �@ �| �P�@ ) �{ (�@�@�@360�� �@ �@ ) ���@(�@�@�@�@�@�@�@93.67..�� �@�@�@�@�@�@ �@ ) �~ ( �@ �| �P�@ ) �{�@360�� ���@�|93.67..���@�{�@360�� ���@�@360���@ �|�@ 93.67�� �@�� cho ���@���@266.32�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� ( 110.77���@���@18 ) ���Y �@���@�ځ@6.153979..�@���Y�@ �@�@�� cho ���@���@�� ( 266.32���@���@36 ) ��turn ���@�ځ@7.397825..�@��turn �@�@ �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@6_.1_5_3_9_7_9.. �@�@�@�@ �� cho ���@�@7._3_9_7_8_2_5.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@67.135937987295..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�ځ@67.135937988206..�@cho�� �@ |
�@�@�@�@�邢�@�@�₵���@�@���ǂ�
�@�@�@�@(�@�ׂ@�́@�y�[�W�@���������@( �t���C�E�S�� ))
�₵��@( ���C�i�[ )�@�@�@�@�@�@�@�@�@�@�@�@ �� ���傤�����@�@�� ���ǂ�
�����イ�@�́@�������@�́@�~�[�g�|�C���g�@�Ɓ@���Ȃ��@( 72.5���� �� )�@�Ɂ@���Ă܂��B
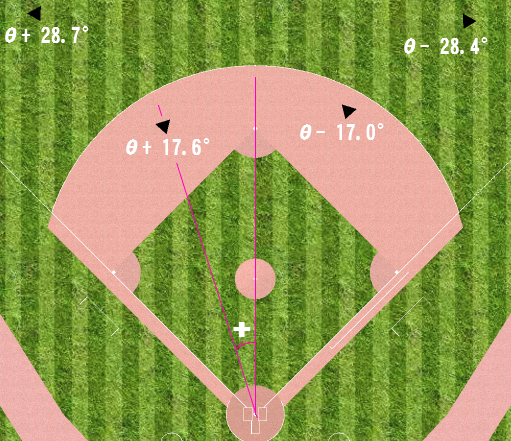
�V���[�g�@ �Ɓ{17.6�}0.3��
�Z�J���h�@ �Ɓ|17.0�}0.2��
���t�g�@�@ �Ɓ{28.7�}0.6��
���C�g�@�@ �Ɓ|28.4�}0.3��
�V���[�g�@ �@ 7.957070707080�@cho���@(��)
�Z�J���h�@ �@ 2.954040404050�@cho��
���t�g�@�@�@17.559040404050�@cho��
���C�g�@�@�@12.557070707080�@cho��
�@�V���[�g�@�@�@�@7.957070707080�@cho�� �@�@�@�@�@( �� �� 0���@���C�i�[�@�Ƃ��� ) �@�@���@���t�g�@����́@����́@�ӂ�ނ��@�Ł@�� �{ 17.6�@�� �@�@�������@�́@�����ւ��@�́@�����イ�@�J�N�h�@���@0�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 17.6���@�~�@cos 0�� ) �@�@�@�@�@�@�@�@���@acos ( 0.953..�@�@�~�@�@1�@�@) �@�@�@�@�@�@�@�@���@acos ( 0.953..�@) �@�@�@�� cho �R�@���@17.6�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� ) �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@�@tan 0���@�@���@|sin 17.6�� | )�~ sign (-( 17.6��))�{ ( 180�� �{180���~ sign (17.6��)) ���@acot (�@�@�@ 0�@�@�@ ���@|�@0.302.. | ) �~ (�@ �| �P �@) �{�@( 180�� �{�@180�� �~ (�@�P�@)) ���@acot (�@�@�@ 0�@�@�@ ���@�@ 0.302..�@ ) �~ (�@ �| �P �@) �{�@( 180�� �{�@180���@�@�@�@ �@ ) ���@acot (�@�@�@ 0�@�@�@�@�@�@�@�@�@ �@�@) �~ (�@ �| �P �@) �{�@( �@�@�@�@�@360���@�@�@�@�@) ���@(�@�@�@�@�@�@�@90���@�@�@�@�@�@�@�@�@) �~ (�@ �| �P �@) �{�@�@360�� ���@( - 90�� )�@�{�@360�� ���@�@ 360���@ �|�@90�� �@�� cho ���@���@270�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (�@17.6���@ ���@18 ) ���Y �@���@�ځ@0.977777..�@���Y�@ �@�@�� cho ���@���@�� (�@270�� �@ ���@36 ) ��turn ���@�ځ@7.500000..�@��turn �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@0_.9_7_7_7_7_7.. �@�@�@�@ �� cho ���@�@7._5_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�� �@ 7.957070707070..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�� �@ 7.957070707080..�@cho�� �@ |
�@�Z�J���h�@�@�@�@2.954040404050�@cho�� �@�@�@�@�@( �� �� 0���@���C�i�[ �Ƃ��� ) �@�@���@���C�g�@����́@����́@�ӂ�ނ��@�Ł@�� �| 17.0�@�� �@�@�������@�́@�����ւ��@�́@�����イ�@�J�N�h�@���@0�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos -17.0���@�~�@cos 0�� ) �@�@�@�@�@�@�@�@���@acos ( 0.956..�@�@�~�@�@1�@�@) �@�@�@�@�@�@�@�@���@acos ( 0.956..�@) �@�@�@�� cho �R�@���@17.0�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� ) �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@�@tan 0���@�@���@|sin-17.0�� | )�~ sign (-(-17.0��))�{ ( 180�� �{180���~ sign(-17.6��)) ���@acot (�@�@�@ 0�@�@�@ ���@| - 0.292.. | ) �~ (�@ �@�P �@ ) �{�@( 180�� �{�@180�� �~ (�@�| �P )) ���@acot (�@�@�@ 0�@�@�@ ���@�@ 0.292..�@ ) �~ (�@ �@�P �@ ) �{�@( 180�� �|�@180���@�@�@�@ �@ ) ���@acot (�@�@�@ 0�@�@�@�@�@�@�@�@�@ �@�@) �~ (�@ �@�P �@ ) �{�@( �@�@�@�@�@�@0�� �@�@�@�@�@) ���@(�@�@�@�@�@�@�@90���@�@�@�@�@�@�@�@�@) �~ (�@ �@�P �@ ) �{�@�@0�� ���@( �@ 90���@)�@�{�@0�� ���@�@�@90�� �@�� cho ���@���@90�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (�@17.0���@ ���@18 ) ���Y �@���@�ځ@0.944444..�@���Y�@ �@�@�� cho ���@���@�� ( �@90���@�@���@36 ) ��turn ���@�ځ@2.500000..�@��turn �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@0_.9_4_4_4_4_4.. �@�@�@�@ �� cho ���@�@2._5_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�� �@ 2.954040404040..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�� �@ 2.954040404050..�@cho�� �@ |
�@���t�g�@�@�@�@17.559040404050�@cho�� �@�@�@�@�@( �� �� 0���@���C�i�[ �Ƃ��� ) �@�@���t�g�@�ق��߂�ւ́@����́@�ӂ�ނ��@�Ł@�� �{ 28.7�@�� �@�@�������@�́@�����ւ��@�́@�����イ�@�J�N�h�@���@0�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos 28.7���@�~�@cos 0�� ) �@�@�@�@�@�@�@�@���@acos ( 0.877..�@�@�~�@�@1�@�@) �@�@�@�@�@�@�@�@���@acos ( 0.877..�@) �@�@�@�� cho �R�@���@28.7�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� ) �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@�@tan 0���@�@���@|sin 28.7�� | )�~ sign (-( 28.7��))�{ ( 180�� �{180���~ sign (28.7��)) ���@acot (�@�@�@ 0�@�@�@ ���@|�@0.480.. | ) �~ (�@ �| �P �@) �{�@( 180�� �{�@180�� �~ (�@�P�@)) ���@acot (�@�@�@ 0�@�@�@ ���@�@ 0.480..�@ ) �~ (�@ �| �P �@) �{�@( 180�� �{�@180���@�@�@�@ �@ ) ���@acot (�@�@�@ 0�@�@�@�@�@�@�@�@�@ �@�@) �~ (�@ �| �P �@) �{�@( �@�@�@�@�@360���@�@�@�@�@) ���@(�@�@�@�@�@�@�@90���@�@�@�@�@�@�@�@�@) �~ (�@ �| �P �@) �{�@�@360�� ���@( - 90�� )�@�{�@360�� ���@�@ 360���@ �|�@90�� �@�� cho ���@���@270�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (�@28.7���@ ���@18 ) ���Y �@���@�ځ@1.594444..�@���Y�@ �@�@�� cho ���@���@�� (�@270�� �@ ���@36 ) ��turn ���@�ځ@7.500000..�@��turn �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@1_.5_9_4_4_4_4.. �@�@�@�@ �� cho ���@�@7._5_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�� �@17.559040404040..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�� �@17.559040404050..�@cho�� �@ |
�@���C�g�@�@�@�@12.557070707080�@cho�� �@�@�@�@�@( �� �� 0���@���C�i�[ �Ƃ��� ) �@�@���C�g�@�ق��߂�ւ́@����́@�ӂ�ނ��@�Ł@�� �| 28.4�@�� �@�@�������@�́@�����ւ��@�́@�����イ�@�J�N�h�@���@0�@�ǁ@�Ł@����Ɂ@�����Ȃ��Ă݂܂��B �@�ɂ����@�ɂā@�݂Ђ炫�@���@���Ƃ߂܂��B �@�@�@�� cho �R�@���@( �� �E ���@�Ł@�ɂ����@) �@ �@�@�@�@�@�@�@�@���@acos ( cos -28.4���@�~�@cos 0�� ) �@�@�@�@�@�@�@�@���@acos ( 0.879..�@�@�~�@�@1�@�@) �@�@�@�@�@�@�@�@���@acos ( 0.879..�@) �@�@�@�� cho �R�@���@28.4�� �@�����炪�@�� cho �R�@( �݂Ђ炫 )�@�Ɂ@�Ȃ�܂��B�@ �c�@�@ �@���@�Ɂ@�X�N�����[�@���@���Ƃ߂܂��B �@�@�@�� cho ���@���@ ( ������ �� ���� �́@���� ) ���@acot (�@�@tan �� �@�@���@|�@sin�@�Ɓ@| ) �~ sign (�@- �� ) �{�@( 180�� �{180���~ sign (�@�Ɓ@)) ���@acot (�@�@tan 0���@�@���@|sin-28.4�� | )�~ sign (-(-28.4��))�{ ( 180�� �{180���~ sign(-28.4��)) ���@acot (�@�@�@ 0�@�@�@ ���@| - 0.475.. | ) �~ (�@ �@�P �@ ) �{�@( 180�� �{�@180�� �~ (�@�| �P )) ���@acot (�@�@�@ 0�@�@�@ ���@�@ 0.475..�@ ) �~ (�@ �@�P �@ ) �{�@( 180�� �|�@180���@�@�@�@ �@ ) ���@acot (�@�@�@ 0�@�@�@�@�@�@�@�@�@ �@�@) �~ (�@ �@�P �@ ) �{�@( �@�@�@�@�@�@0�� �@�@�@�@�@) ���@(�@�@�@�@�@�@�@90���@�@�@�@�@�@�@�@�@) �~ (�@ �@�P �@ ) �{�@�@0�� ���@( �@ 90���@)�@�{�@0�� ���@�@�@90�� �@�� cho ���@���@90�� �@�����炪�@�� cho ���@( �X�N�����[ )�@�Ɂ@�Ȃ�܂��B�@ �c�@�A �@���̂Q�� ( �@ �A )�@�� �R �E�� ���@���@���������@�ł���@�P �ʁ@�Ɂ@�ւ�@���܂��B �@�@�� cho �R�@���@�� (�@28.4���@ ���@18 ) ���Y �@���@�ځ@1.577777..�@���Y�@ �@�@�� cho ���@���@�� ( �@90���@�@���@36 ) ��turn ���@�ځ@2.500000..�@��turn �@���̂Q�@�� �R �E�� ���@���@�������Ɂ@���݂��킹�܂��B �@�@�@�@ �� cho �R �@1_.5_7_7_7_7_7.. �@�@�@�@ �� cho ���@�@2._5_0_0_0_0_0.. �@�@�@�@�@�@�@�@�@�@�@�@���@�@�@�� �@�@�@�@�@�@�@�@�ځ@12.557070707070..�@cho�� ( ���肠����Ȃ� ) �@�@�@�@�@�@�@�@�ځ@12.557070707080..�@cho�� �@ |
�@�@������ �́@�T�C�g�@�́@���傤�ق��@���@�����Ɂ@�|�W�V���j���O�@��
�@�@��������@�ɂā@�ւ����@���� �������� �� �J�N�h�@( �� )�@�� �Ȃ�܂��B
�@�@�������@�́@��������@�����ւ��@�Ł@�����Ȃ��Ă���@( 2D �� )�@�̂ŁA
�@�@����с@��@�ӂ��� ����с@�́@��������@�ɂ́@�Ђт��܂���B
�@�@m(_ _)m