戻る　　下書き　　1　4　7　10　11　12　13

20250415－/uni-text 12

このページ　は　現在　編集中　変更中　調整中

デザイン　・　ネーミング　・　シミュレーション　・　個人的メモ


text--nuance --0416

統合虚数 　 慮 数 　 一時的多重化統合虚数
合成虚数 盲因虚数 　　一時的二重根号化統合虚数
結合虚数 盲因統括虚数 ピタゴラス結合虚数
　　　　　　　　　　　　　　　. 　総和平方合成虚数　. 全虚軸合成虚数
ユナイテッドアイ  ユニコーンアイ ᐂ  多次元暫定一括虚数
 ピタゴラシアンアイ　ᑮ エヌ 次 アイ　ń  maegaki-uni


0.5 + 0.866 ｉ


編集中　変更中　調整中


れいてんご　たす　れいてんはちろくろく　ゆにこーん　あい

0.5 + 0.866 ᐂ



i ＝　√（　i2　） ÷　√1
ᒏ ＝　√（　i2 + j2　） ÷　√2
Ä ＝　√（　i2 + j2 + k2　） ÷　√3
ᐄ ＝　√（　i2 + j2 + k2 + L2　） ÷　√4
ᒌ ＝　√（　i2 + j2 + k2 + L2 + M2　） ÷　√5
ᕣ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2　） ÷　√6
ᔒ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2　） ÷　√7
ᑖ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2　） ÷　√8
ᑏ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2　） ÷　√9
ᐲ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2　） ÷　√10
ᒫ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2　） ÷　√11
ᒦ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2　） ÷　√12
ᒨ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2　） ÷　√13
ᔮ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2　） ÷　√14
ᔫ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2　） ÷　√15
ᕌ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2　） ÷　√16
ᕇ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2　） ÷　√17
ᕉ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2 + Z2　） ÷　√18
ᐂ ＝　√（　i2 ＋（　何種類 かは 不問 のまま 、） … +　必要 に 応 じて 考慮 可能 なかぎり　ふやしていく ） ÷　√　必要数
ϊ ＝　√（　i2 ＋（　１種類 以上 あるかないかの 判断　が　極めて 困難 で、）… +　必要 に 応 じて ふえていく ） ÷　√　必要数
ẅ ＝　√（　i2 + （　１種類 以上 あるかないかの 判断　が　理論的 に 不可能確定 で、） +　必要に応じてふえていく ） ÷　√　必要数
ü ＝　√（　i2 + j2 + （　のように　２種類 以上確定 で、）… +　必要に応じて可能なかぎり　どこまでもふえていく ） ÷　√　２以上 の 必要数
ᑮ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + … + X2 + Y2 + Z2　… +　もっと多い ） ÷　√18 よりも もっと多い 具体的 な すでに 確定している 数
¿ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 … … … … … … … … + X2 + Y2 + Z2　… +　未定　ばんめ ） ÷　√　未定
ń ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2… … … … … … … … … … + X2 + Y2 + Z2　… +　永遠 に ある ） ÷　√　永遠



よみかた



並びかえ中




ᒏ　＝：　√（ -1 ）
Ä　＝：　√（ -1 ）
ᐄ　＝：　√（ -1 ）

↓
：

ϊ　 ＝：　√（ -1 ）






カナディアン　シラバス　ユニコード

ᐄ
ᒌ
ᕣ
ᔒ
ᑖ
ᑏ
ᐲ
ᒫ
ᒦ
ᒨ
ᔮ
ᔫ
ᕌ
ᕇ
ᕉ		   U+1404
U+148c
U+1563
U+1512
U+1456
U+144f
U+1432
U+14ab
U+14a6
U+14a8
U+152e
U+152b
U+154c
U+1547
U+1549

U+ ４ケタ　の　４ケタ 入力 後　「　alt　+　x　」










カナディアン　シラバス　の　りゃく　より

ためしに

「　カナ（●●）　」

を　先 頭　に　つけて

よんでみることに　してみます。


（カナイー）
（カナシー）
（カナジー）　
（カナシュィー）
（カナター）
（カナチー）
（カナピー）
（カナマー）
（カナミー）
（カナモー）
（カナヤー）
（カナヨー）
（カナラー）
（カナリー）
（カナロー）		  　　 0.5 + 0.866 ᐄ
0.5 + 0.866 ᒌ
0.5 + 0.866 ᕣ
0.5 + 0.866 ᔒ
0.5 + 0.866 ᑖ
0.5 + 0.866 ᑏ
0.5 + 0.866 ᐲ
0.5 + 0.866 ᒫ
0.5 + 0.866 ᒦ
0.5 + 0.866 ᒨ
0.5 + 0.866 ᔮ
0.5 + 0.866 ᔫ
0.5 + 0.866 ᕌ
0.5 + 0.866 ᕇ
0.5 + 0.866 ᕉ		  　　. 4D
5D
6D
7D
8D
9D
10D
11D
12D
13D
14D
15D
16D
17D
18D





仮編集中　 …　参照元　の　Unicode　の　称号　は　→　ここ



     仮 オリジナル 虚 数 名

    
 i
ᒏ.
Ä.

ᑮ.

ᐂ .

ń

ü

ẅ

 ϊ

¿

ʝ
 アイ
ジャイ
アジャイ

ピタゴラシアンアイ

ユニコーンアイ

エヌ 次 アイ

ユナイテッドアイ

ワンダーアイ

ニジゲンアイ

ハテナイ

ジェイ クロステイル
 U+0069
U+148f
U+00c4

U+146E

U+1402

U+0144

U+00fc

U+1e85

U+03ca

U+00bf

U+029d
 アルファベット
（カナィクー）
ダイエレシスエー

（カナキー）

（カナアーイ）

アキュートエヌ

トレマユー

ダイヤリテカダブリュ

ダイヤリテカイオタ

インバーテッドクエスチョン

クロステールジェイ

図　編集中
↓






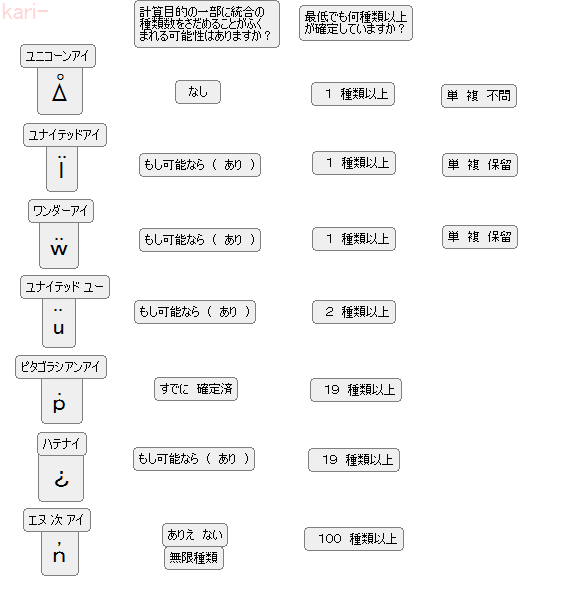編集　変更　調整　中

↓














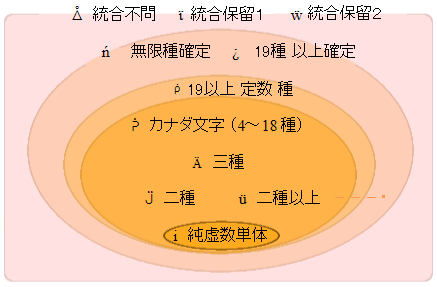
√（　るーと　ひとつに　まとめる　かたち　）



i ＝　√（（　i2　） ÷　1　）
ᒏ ＝　√（（　i2 + j2　） ÷　2　）
Ä ＝　√（（　i2 + j2 + k2　） ÷　3　）
ᐄ ＝　√（（　i2 + j2 + k2 + L2　） ÷　4　）
ᒌ ＝　√（（　i2 + j2 + k2 + L2 + M2　） ÷　5　）
ᕣ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2　） ÷　6　）
ᔒ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2　） ÷　7　）
ᑖ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2　） ÷　8　）
ᑏ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2　） ÷　9　）
ᐲ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2　） ÷　10　）
ᒫ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2　） ÷　11　）
ᒦ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2　） ÷　12　）
ᒨ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2　） ÷　13　）
ᔮ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2　） ÷　14　）
ᔫ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2　） ÷　15　）
ᕌ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2　） ÷　16　）
ᕇ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2　） ÷　17　）
ᕉ ＝　√（（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2 + Z2　） ÷　18　）




×√　⇔　÷√

わりざん右　を　かけざん左　に　うつした　かたち



√1 i ＝　√（　i2　）
√2 ᒏ ＝　√（　i2 + j2　）
√3 Ä ＝　√（　i2 + j2 + k2　）
√4 ᐄ ＝　√（　i2 + j2 + k2 + L2　）
√5 ᒌ ＝　√（　i2 + j2 + k2 + L2 + M2　）
√6 ᕣ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2　）
√7 ᔒ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2　）
√8 ᑖ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2　）
√9 ᑏ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2　）
√10 ᐲ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2　）
√11 ᒫ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2　）
√12 ᒦ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2　）
√13 ᒨ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2　）
√14 ᔮ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2　）
√15 ᔫ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2　）
√16 ᕌ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2　）
√17 ᕇ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2　）
√18 ᕉ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 + U2 + V2 + W2 + X2 + Y2 + Z2　）









しぜんすう　の　くみあわせ　（　ピタゴラス　数　）　での

とうごう　の　いちれい　１　２　３


※　　3i2　※

（　3i　×　3i　の　いみ　）
ただしくは　（　3i　）2


1i2 ＝　1i2
5ᒏ2 ＝　3i2 + 4j2
3Ä2 ＝　1i2 + 2j2 + 2k2
5ᐄ2 ＝　1i2 + 2j2 + 2k2 + 4L2
4ᒌ2 ＝　1i2 + 1j2 + 1k2 + 2L2 + 3M2
5ᕣ2 ＝　1i2 + 1j2 + 1k2 + 2L2 + 3M2 + 3N2
5ᔒ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 2N2 + 4O2
4ᑖ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 3P2
3ᑏ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2
6ᐲ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 2P2 + 3Q2 + 4R2
5ᒫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 2Q2 + 2R2 + 3S2
7ᒦ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 2P2 + 2Q2 + 3R2 + 3S2 + 4T2
5ᒨ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 2R2 + 2S2 + 2T2 + 2U2
7ᔮ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 6V2
6ᔫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 2Q2 + 2R2 + 2S2 + 2T2 + 2U2 + 2V2 + 2W2
4ᕌ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 1V2 + 1W2 + 1X2
5ᕇ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 1V2 + 1W2 + 1X2 + 3Y2
8ᕉ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 2T2 + 2U2 + 3V2 + 3W2 + 3X2 + 3Y2 + 3Z2








盲点　の　要因　 …　「　盲因　」


盲因　ᐂ








　　　小 数 化 での 近 似 値 イメージ　いちれい　　1　2



i 　≒　√（（　1.0000i　）2 ）


ᒏ 　≒　√（（　0.7071i ）2　+　（　0.7071j　）2 ）


Ä 　≒　√（（　0.5774i　）2　+　（　0.5774j　）2　+　（　0.5774k　）2 ）


ᐄ 　≒　√（（　0.5000i　）2　+　（　0.5000j　）2+　（　0.5000k　）2　+　（　0.5000L　）2 ）


ᒌ 　≒　√（（　0.4472i　）2　+　（　0.4472j　）2　+　（　0.4472k　）2　+　（　0.4472L　）2　+　（　0.4472M　）2 ）




ᒏ 　≒　√（（　0.8000i ）2　+　（　0.6000j　）2 ）


ᒏ 　≒　√（（　0.5000i ）2　+　（　0.8660j　）2 ）


ᒏ 　≒　√（（　0.6428i ）2　+　（　0.7660j　）2 ）


ᒏ 　≒　√（（　0.5403i ）2　+　（　0.8415j　）2 ）








しぜんすう　の　くみあわせ　（　ピタゴラス　数　）　での

とうごう　の　いちれい　１　２　３


※　　3i2　※

（　3i　×　3i　の　いみ　）
ただしくは　（　3i　）2


2i2 ＝　2i2
10ᒏ2 ＝　6i2 + 8j2
6Ä2 ＝　2i2 + 4j2 + 4k2
6ᐄ2 ＝　1i2 + 1j2 + 3k2 + 5L2
5ᒌ2 ＝　2i2 + 2j2 + 2k2 + 2L2 + 3M2
3ᕣ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 2N2
4ᔒ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 2M2 + 2N2 + 2O2
5ᑖ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 2M2 + 2N2 + 2O2 + 3P2
5ᑏ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 3P2 + 3Q2
4ᐲ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 2Q2 + 2R2
6ᒫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 2O2 + 2P2 + 2Q2 + 3R2 + 3S2
6ᒦ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 5T2
4ᒨ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 2U2
5ᔮ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 2U2 + 3V2
6ᔫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 2U2 + 2V2 + 4W2
5ᕌ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 2V2 + 2W2 + 2X2
6ᕇ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 1V2 + 2W2 + 3X2 + 3Y2
6ᕉ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 1V2 + 1W2 + 1X2 + 2Y2 + 4Z2












しぜんすう　の　くみあわせ　（　ピタゴラス　数　）　での

とうごう　の　いちれい　１　２　３


※　　3i2　※

（　3i　×　3i　の　いみ　）
ただしくは　（　3i　）2


3i2 ＝　3i2
15ᒏ2 ＝　9i2 + 12j2
7Ä2 ＝　2i2 + 3j2 + 6k2
2ᐄ2 ＝　1i2 + 1j2 + 1k2 + 1L2
6ᒌ2 ＝　1i2 + 1j2 + 3k2 + 3L2 + 4M2
6ᕣ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 4M2 + 4N2
7ᔒ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 2M2 + 4N2 + 5O2
7ᑖ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 2N2 + 2O2 + 6P2
6ᑏ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 2P2 + 5Q2
5ᐲ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 4R2
7ᒫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 2R2 + 6S2
6ᒦ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 3R2 + 3S2 + 3T2
6ᒨ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 3T2 + 4U2
6ᔮ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 2S2 + 2T2 + 3U2 + 3V2
7ᔫ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 2P2 + 2Q2 + 2R2 + 2S2 + 2T2 + 2U2 + 3V2 + 3W2
6ᕌ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 2T2 + 2U2 + 2V2 + 2W2 + 3X2
7ᕇ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 1U2 + 1V2 + 1W2 + 3X2 + 5Y2
8ᕉ2 ＝　1i2 + 1j2 + 1k2 + 1L2 + 1M2 + 1N2 + 1O2 + 1P2 + 1Q2 + 1R2 + 1S2 + 1T2 + 2U2 + 2V2 + 2W2 + 2X2 + 2Y2 + 2Z2











　　　ピタゴラス数　比　小 数 化　での　とうごう　の　いちれい　　1　2




i 　＝　√（（　1.0i　）2 ）


ᒏ 　＝　√（（　0.8i ）2　+　（　0.6j　）2 ）


Ä 　≒　√（（0.666i）2　+　（0.666k）2　+　（0.333L）2 ）


ᐄ 　＝　√（（　0.8i　）2　+　（　0.4j　）2　+　（　0.4k　）2　+　（　0.2L　）2 ）


ᒌ 　＝　√（（　0.6i　）2　+　（　0.4j　）2　+　（　0.4k　）2　+　（　0.4L　）2　+　（　0.4M　）2 ）


ᕣ　＝　√（（　0.6i　）2　+　（　0.6j　）2　+　（　0.4k　）2　+　（　0.2k　）2　+　（　0.2L　）2　+　（　0.2M　）2 ）


ᔒ　＝　√（（　0.8i　）2　+　（　0.4j　）2　+　（　0.2k　）2　+　（　0.2k　）2　+　（　0.2k　）2　+　（　0.2L　）2　+　（　0.2M　）2 ）


ᑖ　＝　√（（　0.6i　）2　+　（　0.4j　）2　+　（　0.4k　）2　+　（　0.4k　）2　+　（　0.2k　）2　+　（　0.2k　）2　+　（　0.2L　）2　+　（　0.2M　）2 ）















（　いち　アイ　＋　えっくす　）　　の　　かたち



i　＝　i
ᒏ　＝　i + 0j
Ä　＝　i + 0j + 0k
ᐄ　＝　i + 0j + 0k + 0L
ᒌ　＝　i + 0j + 0k + 0L + 0M
ᕣ　＝　i + 0j + 0k + 0L + 0M + 0N
ᔒ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O
ᑖ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P
ᑏ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q
ᐲ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R
ᒫ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S
ᒦ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T
ᒨ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U
ᔮ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U + 0V
ᔫ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U + 0V + 0W
ᕌ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U + 0V + 0W + 0X
ᕇ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U + 0V + 0W + 0X + 0Y
ᕉ　＝　i + 0j + 0k + 0L + 0M + 0N + 0O + 0P + 0Q + 0R + 0S + 0T + 0U + 0V + 0W + 0X + 0Y + 0Z











（　統合次元 増設 参考 イメージ　）　　の　　かたち



i　　＝
　
ᒏ　　≒
Ä　　≒
ᐄ　　≒
ᒌ　　≒
ᕣ　　≒
ᔒ　　≒
ᑖ　　≒
ᑏ　　≒
ᐲ　　≒
ᒫ　　≒
ᒦ　　≒
ᒨ　　≒
ᔮ　　≒
ᔫ　　≒
ᕌ　　≒
ᕇ　　≒
ᕉ　　≒		 　 i

　 i
　ᒏ
　Ä
　ᐄ
　ᒌ
　ᕣ
　ᔒ
　ᑖ
　ᑏ
　ᐲ
　ᒫ
　ᒦ
　ᒨ
　ᔮ
　ᔫ
　ᕌ
　ᕇ

　+ 0.000001 j
　+ 0.000001 k
　+ 0.000001 L
　+ 0.000001 M
　+ 0.000001 N
　+ 0.000001 O
　+ 0.000001 P
　+ 0.000001 Q
　+ 0.000001 R
　+ 0.000001 S
　+ 0.000001 T
　+ 0.000001 U
　+ 0.000001 V
　+ 0.000001 W
　+ 0.000001 X
　+ 0.000001 Y
　+ 0.000001 Z
    　+　追加新虚数


0.000001　は　ほぼ ゼロ に　ちかい エネルギー 量　の　と　カイシャク　するとき

左辺　≒　右辺

左　と　右　は　（ 厳密 には　等しいとはいえないものの、）　かなり　ちかい　エネルギー 量　といえます。

0.000001　→　かみくだいて　リミットゼロ （ 無限小 ）




よみかた


もどる

ユニコーンアイ ＝　√（　i2 ＋（　何種類 かは 不問 のまま 、） … +　必要 に 応 じて 考慮 可能 なかぎり　ふやしていく ） ÷　√　必要数

ᐂ ＝　√（　i2 ＋（　何種類 かは 不問 のまま 、） … +　必要 に 応 じて 考慮 可能 なかぎり　ふやしていく ） ÷　√　必要数



ダイヤリテカイオタ ＝　√（　i2 ＋（　１種類 以上 あるかないかの 判断　が　極めて 困難 で、）… +　必要 に 応 じて ふえていく ） ÷　√　必要数

ϊ ＝　√（　i2 ＋（　１種類 以上 あるかないかの 判断　が　極めて 困難 で、）… +　必要 に 応 じて ふえていく ） ÷　√　必要数



ワンダーアイ ＝　√（　i2 + （　１種類 以上 あるかないかの 判断　が　理論的 に 不可能確定 で、） +　必要に応じてふえていく ） ÷　√　必要数

ẅ ＝　√（　i2 + （　１種類 以上 あるかないかの 判断　が　理論的 に 不可能確定 で、） +　必要に応じてふえていく ） ÷　√　必要数



ユナイテッドアイ ＝　√（　i2 + j2 + （　のように　２種類 以上確定 で、）… +　必要に応じて可能なかぎり　どこまでもふえていく ） ÷　√　２以上 の 必要数

ü ＝　√（　i2 + j2 + （　のように　２種類 以上確定 で、）… +　必要に応じて可能なかぎり　どこまでもふえていく ） ÷　√　２以上 の 必要数



ピタゴラシアンアイ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + … + X2 + Y2 + Z2　… +　もっと多い ） ÷　√18 よりも もっと多い 具体的 な すでに 確定している 数

ᑮ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + … + X2 + Y2 + Z2　… +　もっと多い ） ÷　√18 よりも もっと多い 具体的 な すでに 確定している 数



エヌ 次 アイ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 … … … … … … … + X2 + Y2 + Z2　… +　永遠 に ある ） ÷　√　永遠

ń ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2… … … … … … … … … … + X2 + Y2 + Z2　… +　永遠 に ある ） ÷　√　永遠




ハテナイ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2… … … … … … … … … … + X2 + Y2 + Z2　… +　未定　ばんめ ） ÷　√　未定

¿ ＝　√（　i2 + j2 + k2 + L2 + M2 + N2 + O2 + P2 + Q2 + R2 + S2 + T2 … … … … … … … … + X2 + Y2 + Z2　… +　未定　ばんめ ） ÷　√　未定







図　編集中
↓



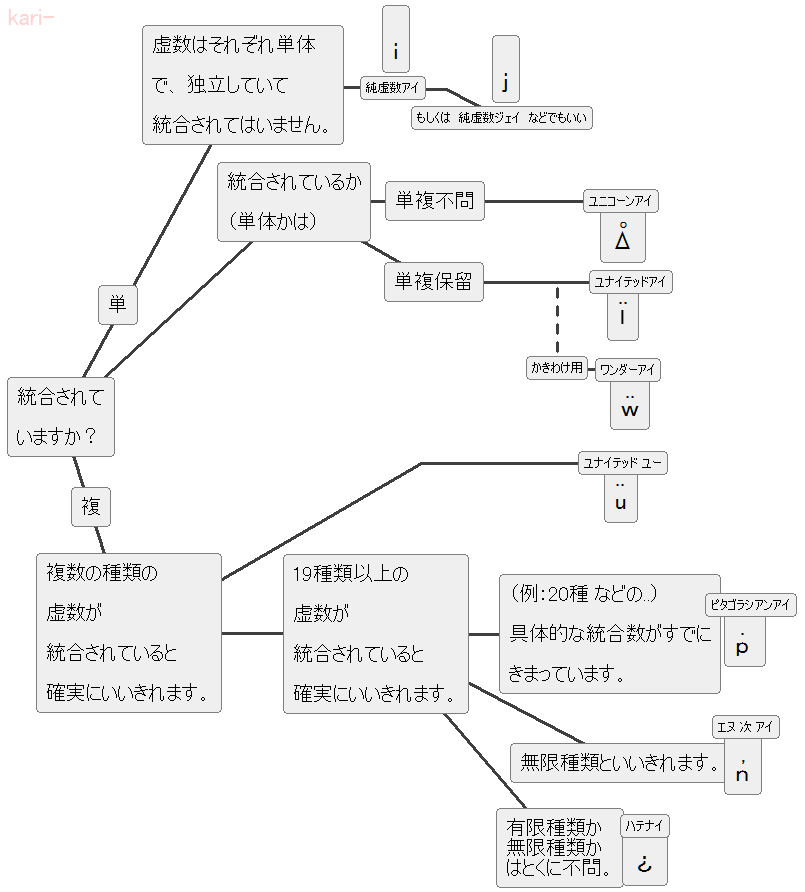●　と　○　との　ニュアンス

未　途中つづき
i ᐂ ϊ ẅ ü ᑮ ń ¿
i 　／　 　●　 　　　 　　　 　　　 　　　 　　　 　　　
ᐂ 　　　 　／　 　　　 　　　 　　　 　　　 　　　 　　　
ϊ 　　　 　　　 　／　 　　　 　　　 　　　 　　　 　　　
ẅ 　　　 　　　 　　　 　／　 　　　 　　　 　　　 　　　
ü 　　　 　　　 　　　 　　　 　／　 　　　 　　　 　　　
ᑮ 　　　 　　　 　　　 　　　 　　　 　／　 　　　 　　　
ń 　　　 　　　 　　　 　　　 　　　 　　　 　／　 　　　
¿
















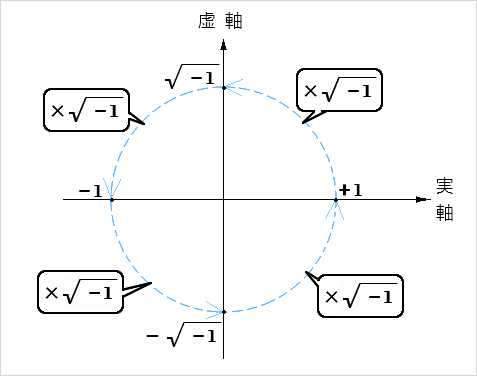▼　□　□　□　□　□　□　□　□　□　□　□　□　□　□　□　　もどる


i 2　＝ 　－1
j 2　＝ 　－1
ᒏ 2　＝ 　－1
Ä 2　＝ 　－1
ᐄ 2　＝ 　－1
ᒌ 2　＝ 　－1
ᕣ 2　＝ 　－1
ᔒ 2　＝ 　－1
ᑖ 2　＝ 　－1
ᑏ 2　＝ 　－1
ᐲ 2　＝ 　－1
ᒫ 2　＝ 　－1
ᒦ 2　＝ 　－1
ᒨ 2　＝ 　－1
ᔮ 2　＝ 　－1
ᔫ 2　＝ 　－1
ᕌ 2　＝ 　－1
ᕇ 2　＝ 　－1
ᕉ 2　＝ 　－1




□　▼　□　□　□　□　□　□　□　□　□　□　□　□　□　□　　もどる


i　× i　＝ 　－1
j　× j　＝ 　－1
ᒏ　× ᒏ　＝ 　－1
Ä　× Ä　＝ 　－1
ᐄ　× ᐄ　＝ 　－1
ᒌ　× ᒌ　＝ 　－1
ᕣ　× ᕣ　＝ 　－1
ᔒ　× ᔒ　＝ 　－1
ᑖ　× ᑖ　＝ 　－1
ᑏ　× ᑏ　＝ 　－1
ᐲ　× ᐲ　＝ 　－1
ᒫ　× ᒫ　＝ 　－1
ᒦ　× ᒦ　＝ 　－1
ᒨ　× ᒨ　＝ 　－1
ᔮ　× ᔮ　＝ 　－1
ᔫ　× ᔫ　＝ 　－1
ᕌ　× ᕌ　＝ 　－1
ᕇ　× ᕇ　＝ 　－1
　　　　　　＿ᕉ　× ᕉ　＝ 　－1




□　□　▼　□　□　□　□　□　□　□　□　□　□　□　□　□　　もどる


2i 2　＝ 　－2
2j 2　＝ 　－2
2ᒏ 2　＝ 　－2
2Ä 2　＝ 　－2
2ᐄ 2　＝ 　－2
2ᒌ 2　＝ 　－2
2ᕣ 2　＝ 　－2
2ᔒ 2　＝ 　－2
2ᑖ 2　＝ 　－2
2ᑏ 2　＝ 　－2
2ᐲ 2　＝ 　－2
2ᒫ 2　＝ 　－2
2ᒦ 2　＝ 　－2
2ᒨ 2　＝ 　－2
2ᔮ 2　＝ 　－2
2ᔫ 2　＝ 　－2
2ᕌ 2　＝ 　－2
2ᕇ 2　＝ 　－2
2ᕉ 2　＝ 　－2




□　□　□　▼　□　□　□　□　□　□　□　□　□　□　□　□　　もどる


2　×　 i　× i　＝ 　－2
2　×　 j　× j　＝ 　－2
2　×　 ᒏ　× ᒏ　＝ 　－2
2　×　 Ä　× Ä　＝ 　－2
2　×　 ᐄ　× ᐄ　＝ 　－2
2　×　 ᒌ　× ᒌ　＝ 　－2
2　×　 ᕣ　× ᕣ　＝ 　－2
2　×　 ᔒ　× ᔒ　＝ 　－2
2　×　 ᑖ　× ᑖ　＝ 　－2
2　×　 ᑏ　× ᑏ　＝ 　－2
2　×　 ᐲ　× ᐲ　＝ 　－2
2　×　 ᒫ　× ᒫ　＝ 　－2
2　×　 ᒦ　× ᒦ　＝ 　－2
2　×　 ᒨ　× ᒨ　＝ 　－2
2　×　 ᔮ　× ᔮ　＝ 　－2
2　×　 ᔫ　× ᔫ　＝ 　－2
2　×　 ᕌ　× ᕌ　＝ 　－2
2　×　 ᕇ　× ᕇ　＝ 　－2
　　2　×　 ᕉ　× ᕉ　＝ 　－2




□　□　□　□　▼　□　□　□　□　□　□　□　□　□　□　□　　もどる


(　2 i　) 2　＝ 　－4
(　2 j　) 2　＝ 　－4
(　2ᒏ　) 2　＝ 　－4
(　2Ä　) 2　＝ 　－4
(　2ᐄ　) 2　＝ 　－4
(　2ᒌ　) 2　＝ 　－4
(　2ᕣ　) 2　＝ 　－4
(　2ᔒ　) 2　＝ 　－4
(　2ᑖ　) 2　＝ 　－4
(　2ᑏ　) 2　＝ 　－4
(　2ᐲ　) 2　＝ 　－4
(　2ᒫ　) 2　＝ 　－4
(　2ᒦ　) 2　＝ 　－4
(　2ᒨ　) 2　＝ 　－4
(　2ᔮ　) 2　＝ 　－4
(　2ᔫ　) 2　＝ 　－4
(　2ᕌ　) 2　＝ 　－4
(　2ᕇ　) 2　＝ 　－4
(　2ᕉ　) 2　＝ 　－4








□　□　□　□　□　▼　□　□　□　□　□　□　□　□　□　□　　もどる


2　×　 i × 2　×　 i ＝ 　－4
2　×　 j × 2　×　 j ＝ 　－4
2　×　ᒏ × 2　×　ᒏ ＝ 　－4
2　×　Ä × 2　×　Ä ＝ 　－4
2　×　ᐄ × 2　×　ᐄ ＝ 　－4
2　×　ᒌ × 2　×　ᒌ ＝ 　－4
2　×　ᕣ × 2　×　ᕣ ＝ 　－4
2　×　ᔒ × 2　×　ᔒ ＝ 　－4
2　×　ᑖ × 2　×　ᑖ ＝ 　－4
2　×　ᑏ × 2　×　ᑏ ＝ 　－4
2　×　ᐲ × 2　×　ᐲ ＝ 　－4
2　×　ᒫ × 2　×　ᒫ ＝ 　－4
2　×　ᒦ × 2　×　ᒦ ＝ 　－4
2　×　ᒨ × 2　×　ᒨ ＝ 　－4
2　×　ᔮ × 2　×　ᔮ ＝ 　－4
2　×　ᔫ × 2　×　ᔫ ＝ 　－4
2　×　ᕌ × 2　×　ᕌ ＝ 　－4
2　×　ᕇ × 2　×　ᕇ ＝ 　－4
2　×　ᕉ × 2　×　ᕉ ＝ 　－4




□　□　□　□　□　□　▼　□　□　□　□　□　□　□　□　□　　もどる


i 3　＝ 　－i
j 3　＝ 　－j
ᒏ 3　＝ 　－ᒏ
Ä 3　＝ 　－Ä
ᐄ 3　＝ 　－ᐄ
ᒌ 3　＝ 　－ᒌ
ᕣ 3　＝ 　－ᕣ
ᔒ 3　＝ 　－ᔒ
ᑖ 3　＝ 　－ᑖ
ᑏ 3　＝ 　－ᑏ
ᐲ 3　＝ 　－ᐲ
ᒫ 3　＝ 　－ᒫ
ᒦ 3　＝ 　－ᒦ
ᒨ 3　＝ 　－ᒨ
ᔮ 3　＝ 　－ᔮ
ᔫ 3　＝ 　－ᔫ
ᕌ 3　＝ 　－ᕌ
ᕇ 3　＝ 　－ᕇ
ᕉ 3　＝ 　－ᕉ




□　□　□　□　□　□　□　▼　□　□　□　□　□　□　□　□　　もどる


i　× i　× i　＝ 　－i
j　× j　× j　＝ 　－j
ᒏ　× ᒏ　× ᒏ　＝ 　－ᒏ
Ä　× Ä　× Ä　＝ 　－Ä
ᐄ　× ᐄ　× ᐄ　＝ 　－ᐄ
ᒌ　× ᒌ　× ᒌ　＝ 　－ᒌ
ᕣ　× ᕣ　× ᕣ　＝ 　－ᕣ
ᔒ　× ᔒ　× ᔒ　＝ 　－ᔒ
ᑖ　× ᑖ　× ᑖ　＝ 　－ᑖ
ᑏ　× ᑏ　× ᑏ　＝ 　－ᑏ
ᐲ　× ᐲ　× ᐲ　＝ 　－ᐲ
ᒫ　× ᒫ　× ᒫ　＝ 　－ᒫ
ᒦ　× ᒦ　× ᒦ　＝ 　－ᒦ
ᒨ　× ᒨ　× ᒨ　＝ 　－ᒨ
ᔮ　× ᔮ　× ᔮ　＝ 　－ᔮ
ᔫ　× ᔫ　× ᔫ　＝ 　－ᔫ
ᕌ　× ᕌ　× ᕌ　＝ 　－ᕌ
ᕇ　× ᕇ　× ᕇ　＝ 　－ᕇ
　　　　　　＿ᕉ　× ᕉ　× ᕉ　＝ 　－ᕉ




□　□　□　□　□　□　□　□　▼　□　□　□　□　□　□　□　　もどる


2i 3　＝ 　－2 i
2j 3　＝ 　－2 j
2ᒏ 3　＝ 　－2ᒏ
2Ä 3　＝ 　－2Ä
2ᐄ 3　＝ 　－2ᐄ
2ᒌ 3　＝ 　－2ᒌ
2ᕣ 3　＝ 　－2ᕣ
2ᔒ 3　＝ 　－2ᔒ
2ᑖ 3　＝ 　－2ᑖ
2ᑏ 3　＝ 　－2ᑏ
2ᐲ 3　＝ 　－2ᐲ
2ᒫ 3　＝ 　－2ᒫ
2ᒦ 3　＝ 　－2ᒦ
2ᒨ 3　＝ 　－2ᒨ
2ᔮ 3　＝ 　－2ᔮ
2ᔫ 3　＝ 　－2ᔫ
2ᕌ 3　＝ 　－2ᕌ
2ᕇ 3　＝ 　－2ᕇ
2ᕉ 3　＝ 　－2ᕉ




□　□　□　□　□　□　□　□　□　▼　□　□　□　□　□　□　　もどる


2　×　 i　× i　× i　＝ 　－2 i
2　×　 j　× j　× j　＝ 　－2 j
2　×　 ᒏ　× ᒏ　× ᒏ　＝ 　－2ᒏ
2　×　 Ä　× Ä　× Ä　＝ 　－2Ä
2　×　 ᐄ　× ᐄ　× ᐄ　＝ 　－2ᐄ
2　×　 ᒌ　× ᒌ　× ᒌ　＝ 　－2ᒌ
2　×　 ᕣ　× ᕣ　× ᕣ　＝ 　－2ᕣ
2　×　 ᔒ　× ᔒ　× ᔒ　＝ 　－2ᔒ
2　×　 ᑖ　× ᑖ　× ᑖ　＝ 　－2ᑖ
2　×　 ᑏ　× ᑏ　× ᑏ　＝ 　－2ᑏ
2　×　 ᐲ　× ᐲ　× ᐲ　＝ 　－2ᐲ
2　×　 ᒫ　× ᒫ　× ᒫ　＝ 　－2ᒫ
2　×　 ᒦ　× ᒦ　× ᒦ　＝ 　－2ᒦ
2　×　 ᒨ　× ᒨ　× ᒨ　＝ 　－2ᒨ
2　×　 ᔮ　× ᔮ　× ᔮ　＝ 　－2ᔮ
2　×　 ᔫ　× ᔫ　× ᔫ　＝ 　－2ᔫ
2　×　 ᕌ　× ᕌ　× ᕌ　＝ 　－2ᕌ
2　×　 ᕇ　× ᕇ　× ᕇ　＝ 　－2ᕇ
　　2　×　 ᕉ　× ᕉ　× ᕉ　＝ 　－2ᕉ




□　□　□　□　□　□　□　□　□　□　▼　□　□　□　□　□　　もどる


(　2 i　) 3　＝ 　－8
(　2 j　) 3　＝ 　－8
(　2ᒏ　) 3　＝ 　－8
(　2Ä　) 3　＝ 　－8
(　2ᐄ　) 3　＝ 　－8
(　2ᒌ　) 3　＝ 　－8
(　2ᕣ　) 3　＝ 　－8
(　2ᔒ　) 3　＝ 　－8
(　2ᑖ　) 3　＝ 　－8
(　2ᑏ　) 3　＝ 　－8
(　2ᐲ　) 3　＝ 　－8
(　2ᒫ　) 3　＝ 　－8
(　2ᒦ　) 3　＝ 　－8
(　2ᒨ　) 3　＝ 　－8
(　2ᔮ　) 3　＝ 　－8
(　2ᔫ　) 3　＝ 　－8
(　2ᕌ　) 3　＝ 　－8
(　2ᕇ　) 3　＝ 　－8
(　2ᕉ　) 3　＝ 　－8




□　□　□　□　□　□　□　□　□　□　□　▼　□　□　□　□　　もどる


(　2 i　) 2　＝ 　－4

2　×　 i × 2　×　 i ＝ 　－4


－4　…→　こちら 2 より　　　　　..

　－4 × 2　×　 i ＝ 　－8
　－4 × 2　×　 j ＝ 　－8
　－4 × 2　×　ᒏ ＝ 　－8
　－4 × 2　×　Ä ＝ 　－8
　－4 × 2　×　ᐄ ＝ 　－8
　－4 × 2　×　ᒌ ＝ 　－8
　－4 × 2　×　ᕣ ＝ 　－8
　－4 × 2　×　ᔒ ＝ 　－8
　－4 × 2　×　ᑖ ＝ 　－8
　－4 × 2　×　ᑏ ＝ 　－8
　－4 × 2　×　ᐲ ＝ 　－8
　－4 × 2　×　ᒫ ＝ 　－8
　－4 × 2　×　ᒦ ＝ 　－8
　－4 × 2　×　ᒨ ＝ 　－8
　－4 × 2　×　ᔮ ＝ 　－8
　－4 × 2　×　ᔫ ＝ 　－8
　－4 × 2　×　ᕌ ＝ 　－8
　－4 × 2　×　ᕇ ＝ 　－8
　－4 × 2　×　ᕉ ＝ 　－8




□　□　□　□　□　□　□　□　□　□　□　□　▼　□　□　□　　もどる


i 4　＝ 　＋1
j 4　＝ 　＋1
ᒏ 4　＝ 　＋1
Ä 4　＝ 　＋1
ᐄ 4　＝ 　＋1
ᒌ 4　＝ 　＋1
ᕣ 4　＝ 　＋1
ᔒ 4　＝ 　＋1
ᑖ 4　＝ 　＋1
ᑏ 4　＝ 　＋1
ᐲ 4　＝ 　＋1
ᒫ 4　＝ 　＋1
ᒦ 4　＝ 　＋1
ᒨ 4　＝ 　＋1
ᔮ 4　＝ 　＋1
ᔫ 4　＝ 　＋1
ᕌ 4　＝ 　＋1
ᕇ 4　＝ 　＋1
ᕉ 4　＝ 　＋1

いずれも　４ 乗　すると　１　に　なります

統 合 虚 数　　は　いずれも　【　「 ＋１ 」　の　４ 乗 根　】　と　いえます。

ていねいに　いうと 、そのなかでも　「 ＋１ 」　の　原 始 ４ 乗 根




□　□　□　□　□　□　□　□　□　□　□　□　□　▼　□　□　　もどる


虚数　× 虚数　＝ 　－1

－1　× －1　＝ 　＋1


i 2　× i 2　＝ 　＋1
j 2　× j 2　＝ 　＋1
ᒏ 2　× ᒏ 2　＝ 　＋1
Ä 2　× Ä 2　＝ 　＋1
ᐄ 2　× ᐄ 2　＝ 　＋1
ᒌ 2　× ᒌ 2　＝ 　＋1
ᕣ 2　× ᕣ 2　＝ 　＋1
ᔒ 2　× ᔒ 2　＝ 　＋1
ᑖ 2　× ᑖ 2　＝ 　＋1
ᑏ 2　× ᑏ 2　＝ 　＋1
ᐲ 2　× ᐲ 2　＝ 　＋1
ᒫ 2　× ᒫ 2　＝ 　＋1
ᒦ 2　× ᒦ 2　＝ 　＋1
ᒨ 2　× ᒨ 2　＝ 　＋1
ᔮ 2　× ᔮ 2　＝ 　＋1
ᔫ 2　× ᔫ 2　＝ 　＋1
ᕌ 2　× ᕌ 2　＝ 　＋1
ᕇ 2　× ᕇ 2　＝ 　＋1
　　　　　　＿ᕉ 2　× ᕉ 2　＝ 　＋1




□　□　□　□　□　□　□　□　□　□　□　□　□　□　▼　□　　もどる


(　2 i　) 4　＝ 　＋16
(　2 j　) 4　＝ 　＋16
(　2ᒏ　) 4　＝ 　＋16
(　2Ä　) 4　＝ 　＋16
(　2ᐄ　) 4　＝ 　＋16
(　2ᒌ　) 4　＝ 　＋16
(　2ᕣ　) 4　＝ 　＋16
(　2ᔒ　) 4　＝ 　＋16
(　2ᑖ　) 4　＝ 　＋16
(　2ᑏ　) 4　＝ 　＋16
(　2ᐲ　) 4　＝ 　＋16
(　2ᒫ　) 4　＝ 　＋16
(　2ᒦ　) 4　＝ 　＋16
(　2ᒨ　) 4　＝ 　＋16
(　2ᔮ　) 4　＝ 　＋16
(　2ᔫ　) 4　＝ 　＋16
(　2ᕌ　) 4　＝ 　＋16
(　2ᕇ　) 4　＝ 　＋16
(　2ᕉ　) 4　＝ 　＋16





－4　…→　こちら 2 より　　　　　..

２ 乗　× ２ 乗　＝ 　４ 乗

□　□　□　□　□　□　□　□　□　□　□　□　□　□　□　▼　　もどる


　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16
　－4 × 　－4 ＝ 　＋16













――――――――――――――――――――――――――――――――――――

参照 　もどる


ピタゴラシアンアイ　 ᑮ　　カナダの音節体系Kii　　Canadian Syllabics Kii

　　ユニコーンアイ　　ᐂ　　カナダの音節体系Aai　　Canadian Syllabics Aai

 i
ᒏ
Ä

ń
ü

ẅ
 ϊ

¿
ʝ
 U+0069
U+148f
U+00c4

U+0144
U+00fc
U+00fc
U+1e85
U+03ca

U+00bf
U+029d
 - -
カナダのシラバスY-Cree Coo
分音記号付きラテン小文字a

急性ラテン文字N
ツードットのユー
トレマ付きU
分音記号付きラテン小文字W
Dialytikaとギリシャの小文字イオタ ϊ

逆疑問符
クロステール付きラテン小文字J
 		  - -

ä U+00E4Latin Small Letter a with Diaeresis
ダイエレシス（diaeresis）とは、（¨）
Latin Small Letter N with Acute
分音符付きラテン小文字U
ウムラウト付きU
Latin Small Letter W with Diaeresis
ダイヤリテカイオタ ϊ

Inverted Question Mark
Latin Small Letter J with Crossed-Tail


メモ帳　・　オフィス　・　エクスプローラ　 ＯＫ　→　クローム　と　エッジ　 …　△　文字ズレ

　ẍ　U+1e8d
　ṅ　U+1e45
　ṙ　U+1e59
　ṫ　U+1e6b



「　平面　に　」　おとしこむ


３Ｄ空間　三次元空間　を　→　三次元平面　に

４Ｄ空間　四次元空間　を　→　四次元平面　に

５Ｄ空間　五次元空間　を　→　五次元平面　に

６Ｄ空間　六次元空間　を　→　六次元平面　に
：

１０Ｄ空間　十次元空間　を　→　十次元平面　に。

１００Ｄ空間　百次元空間　を　→　百次元平面　に　。


というように

「　２Ｄ平面　に　」　の　かたち　に　おきかえて　まとめます


まとめるさい(　統合時　)　に　√○＾2　なので　

それぞれの　虚軸　の　±符号　情報　は

うしなられます。(＋で 統一されます)

(　いいかたを　かえると　逆回転　も　正回転　に　まとめられます　)

が、

∠　ひらき　を　もとめる　計算　には　影響　しません。

(　同じ　カクド　が　もとまります　)







「　¿　」 に　おける　「　永遠 ÷　√　永遠　」　について　→　
任意　の　数　になりえる　説　を　引用