シート３　　　≪　もどる　　　りん　　てん　　もん　　めん　　えん　　みん　　うん　　げん　　　つぎへ　≫　　　あーく　　　ぜんたい

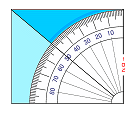
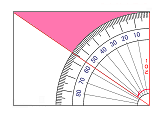
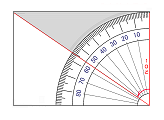
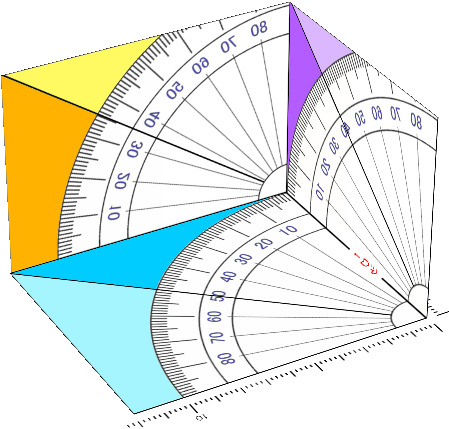
２Ｄ 　３Ｄ	にみんかく 　∠　５５.５５　ど 　カクド　　と　　ヒリツ 　　にみんかく　　 は　　あおいろ　　 と　　　ももいろ 　 を　つかいます 　　かみくだくと　「　にじげん　」　が　「　さんじげん 　で　かつやく　する　わりあい　」　と　たとえてみます 　　つうしょう　は　　「　つーでぃー あーる　」　　と　　「　すりーでぃー あーる　」　　と　かくことにしています　） 　　　（　「　はこがた　」　に　おきかえたので　　はんけい　　が　　たいかくせん　　の　ながさ　に　かわります　） 　　かくど きごう　は　　しーた　Θ 　 と　　２Ｄ ： ３Ｄ　の　ひりつ　 ｒ　 ぱーせんと　を　つかいます 　　この　ふたつ　を　つかい　はいいろ　の　∠　ひらき　（ ５５.５５°）　を　かくにんします その　ながさ　（ あーる ）　の　ひりつ　ぱーせんてーじ ％　の　ことを　「　あーるひ　」　と　よぶことにします きほんてきに　は　０～１００％　いない　で　もとめる　こと　が　こんせぷと　になります （　しかし、　ばあい　によっては　１００％　を　こす　ばあい　（＝　２Ｄ　の　ほうが　つよかった）　という　ことも　おこりえます　） （　マイナス　の　％　の　ばあいは　２Ｄ　と　３Ｄ　が　９０ど　いじょう　ひらきが　あることを　いみしています） 　↑　この　ばあい　 （　２Ｄ　から　３Ｄに　ちかづけていく　つもりなら、なにかしらの　もうてん　を　さぐる　ことが　ひつよう　かもしれません　） 　　にみんかく　では　きいろ　と　むらさきいろ　の　かくど　じょうほう　は　とくに　ひつよう　としません
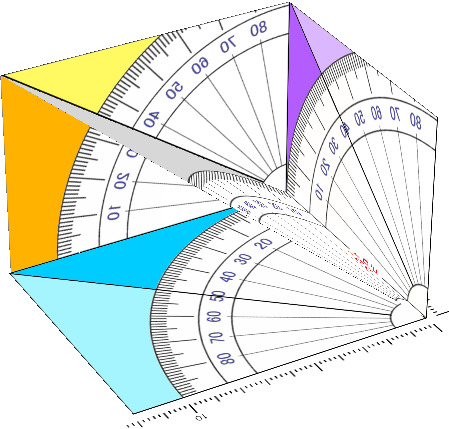
	くみたて 　　まず　シート１　で　はこ　を　つくります 　　シート３　の　ももいろ　は　とくに　きりとる　ひつよう　は　ありません 　　はいいろ　と　ももいろ　は　おなじ　おおきさに　なっていて　そちら　と 　　はこ　を　じょうぎ　に　そわせます
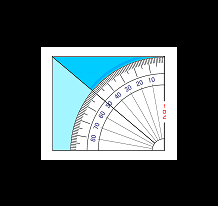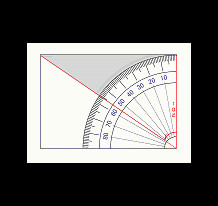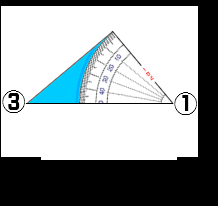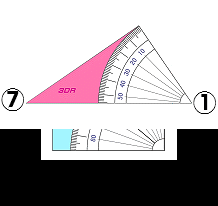
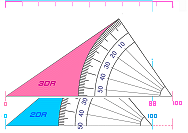
	けいそく 　ひとつめ　は　　Θ　カクド 　　あおいろ　　しーた　の　∠　　５０　　ど　 を　かくにん　します 　ふたつめ　は　　ヒリツ　％ （　も　ど　る　） 　　パーセンテージ　めもり　にて　　③①　と　⑦①　の　　な が さ　　　を　くらべて １００％ ▲　８８％ 　　　　 ８８　％　まで　「　ひ り つ　」　　が　ある　ことを　かくにん　します 　　　　または、 　　　　こさいん　　「　ぷさい　（　あかいろ　）　」　　　　　ＣＯＳ　２８.３４ °　＝　　０.８８０.. 　　　　または、 　　　　さいん　　　「　ふぁい　（　みどりいろ　）」　　　　　　ＳＩＮ　６１.６６ °　＝　　０.８８０.. 　　で、　しょうすうち　が　もとまります　　▽　　　　　　　　　　　　　　　　　　（　＝　８８ ％　） 　　　　※　ぱーせんてーじ　なので　１００　ばい　すると　　あーる　に　なります　 　　- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - （　も　ど　る　）
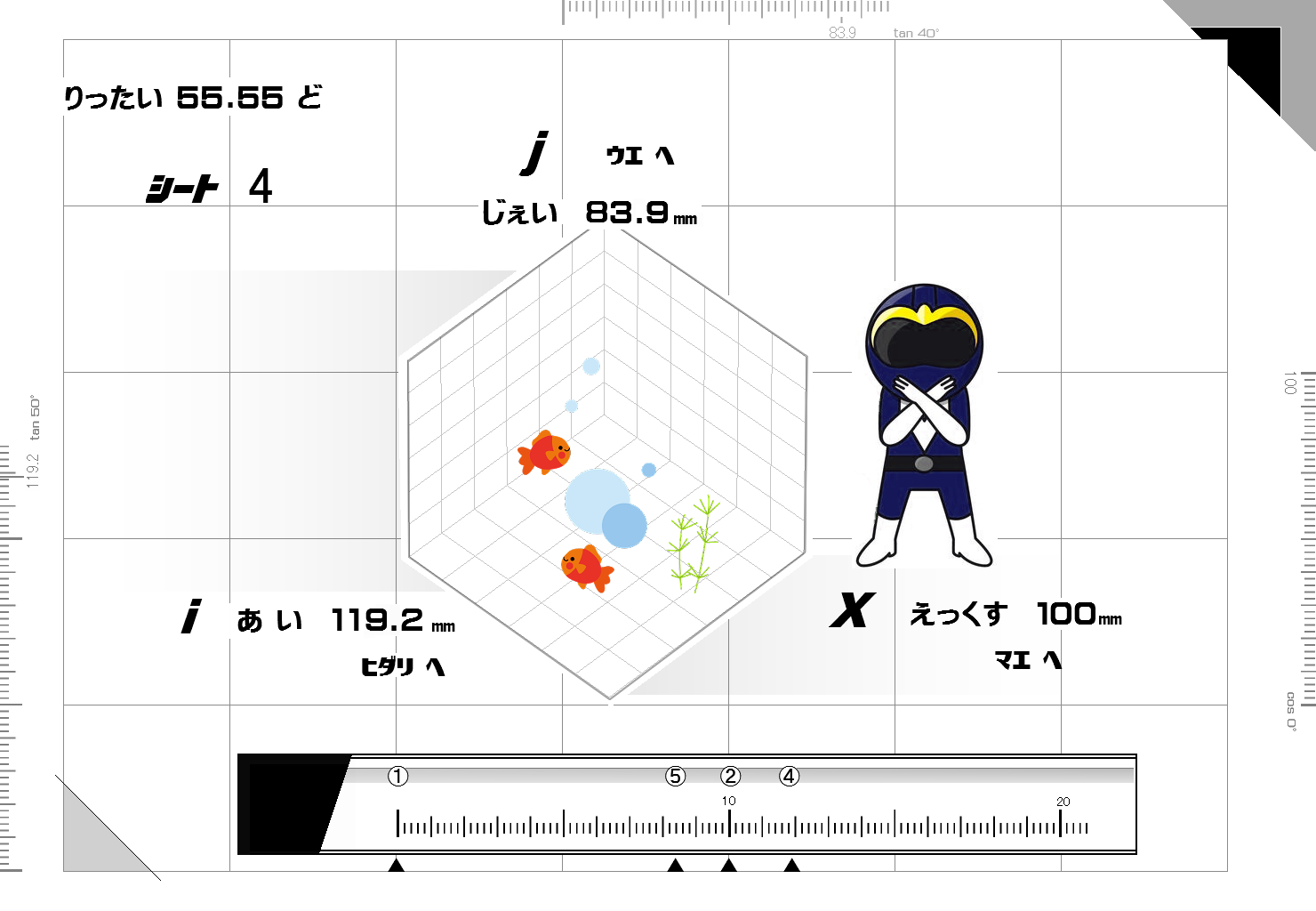	「　ながさ　」　に　ついて … 　　パーセンテージ　めもり 　を　つかわずに　　シート ４　　　でも　くらべられます 　　あおいろ　と　ももいろ　の　たいかくせん　の　ながさ　を　みり　めもり　にて　みくらべます 　 ひとつめ　は 　　あおいろ　の　１５５　みり　めもり　を　かくにん　します 　　せかんと　　「　しーた　（　あおいろ　） 」　　　　　ＳＥＣ　５０ °　　　＝　１.５５５７.. 　ふたつめ　は 　　ももいろ　の　１７６　みり　めもり　を　かくにん　します 　　せかんと　　「　みん　　（　ももいろ　） 」　　　　　ＳＥＣ　５５.５５ ° 　＝　１.７６７７.. 　　（　せかんと　＝　１　÷　こさいん　）　＿ 　　で、　もとまります 　　 たいかくせん　の　ながさ　が　８８ ％　の　ひりつ　になっている　ことを　（　わりざん　で　）　かくにん　します 　　　１５５　÷　１７６　　≒　　およそ　８８ ％ （　も　ど　る　） 　　　また 、　「　きゅうたい　（ はんけい ）」　で　かんがえる　なら、　こさいん　でも　いけます 　　こさいん　　「　しーた　（　あおいろ　） 」　　　　　ＣＯＳ　５０ °　　　 ＝　０.６４２７.. 　　こさいん　　「　みん　　（　ももいろ　） 」　　　　　ＣＯＳ　５５.５５ °　 ＝　０.５６５６.. 　　　５６.５　÷　６４.２　　≒　　およそ　８８ ％ 　　でも、 ひりつ　を　だせます 　「　わるじゅんばん　÷　が　　ぎゃく　」　に　なるだけです 　　※　きじゅん　が　１００　みり　めもり　なので　１００　ばい　すると　　Ｒ　の　ながさ　が　でます
ダウンロード＿	この　２つ　（　カクド　と　ヒリツ　）　を　つかって 　　はいいろ　りったい　かく　　を　もとめる　けいさん　が 　　にみんかく　になります 　　この　さんぷる　では　それが　　∠　５５.５５　ど　　に　なっている　こと　を　かくにん　します
	あーく　にみん あーる 　（　かみくだくと　２じげん　が　３じげん　で　はきっされている　パーセンテージ　を　しらべる　けいさん　になります　） 　　が　さいとこんせぷと　で　とくに　じゅうよう　な　ものの　ひとつ　になります
	のびちじみ　　マジックハンド　　はしごしゃクレーン　　など　.. 　　マジックハンド　の　ながさ　が　３ＤＲ　（ さんじげん　はんけい ）　に　なります クリ　を　マジックハンド　で　おとすとします　　（　３Ｄ　） クリ　が　じめん　に　おちます　（　２Ｄ　） これで　たかさ　の　じげん　が　なくなります クリ　まで　の　きょり　が　すこし　ちかく　なります マジックハンド　を　すこしみじかくして　（ ８８ ％ ）　ひろいます

そのほか


あーるひ = ８８ ％ ＝ 0.88.. ＝cos 28.34 deg ＝ sin 61.66 deg　＝　ぷさい　ふぁい　を　ひもとくと　↓

=　cos （ atan （ cos 50 deg * tan 40 deg ））

=　sin　（ acot （ cos 50 deg * tan 40 deg ））　　　　=　0.88..　←　こっちらなど　でも　もとまります

しょとうてき　かんい　いめーじ　せつめい　（　でふぉると　せってい　）　

みん）　だけ　きじゅん　にする　ながさ　が　かわります　　　 …（　３ＤＲ　＝　１　＝　１００％　）

シート３　　　≪　もどる　　　りん　　てん　　もん　　めん　　えん　　みん　　うん　　げん　　　つぎへ　≫　　ぜんたい